
【题目】已知双曲线![]() 的右顶点到其一条渐近线的距离等于
的右顶点到其一条渐近线的距离等于![]() ,抛物线
,抛物线![]() 的焦点与双曲线
的焦点与双曲线![]() 的右焦点重合,则抛物线
的右焦点重合,则抛物线![]() 上的动点
上的动点![]() 到直线
到直线![]() 和
和![]() 的距离之和的最小值为__________.
的距离之和的最小值为__________.
科目:高中数学 来源: 题型:
【题目】某市统计局就某地居民的月收入调查了10000人,并根据所得数据画出样本的频率分布直方图,每个分组包括左端点,不包括右端点,如第一组表示收入在![]() .
.
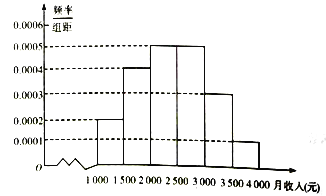
(1)求居民收入在![]() 的频率;
的频率;
(2)根据频率分布直方图算出样本数据的中位数、平均数及其众数;
(3)为了分析居民的收入与年龄、职业等方面的关系,从这10000人中用分层抽样方法抽出100人作进一步分析,则应月收入为![]() 的人中抽取多少人?
的人中抽取多少人?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() ,
,![]() .设
.设![]() 分别为
分别为![]() 中点.
中点.
(1)求证:![]() 平面
平面![]() ;
;
(2)求证:![]() 平面
平面![]() ;
;
(3)试问在线段![]() 上是否存在点
上是否存在点![]() ,使得过三点
,使得过三点![]() 的平面内的任一条直线都与平面
的平面内的任一条直线都与平面![]() 平行?
平行?
若存在,指出点![]() 的位置并证明;若不存在,请说明理由.
的位置并证明;若不存在,请说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,椭圆
中,椭圆![]() 的离心率为
的离心率为![]() ,右顶点为
,右顶点为![]() ,直线
,直线![]() 过原点
过原点![]() ,且点
,且点![]() 在x轴的上方,直线
在x轴的上方,直线![]() 与
与![]() 分别交直线
分别交直线![]() :
: ![]() 于点
于点![]() 、
、![]() .
.
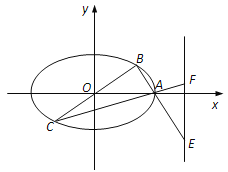
(1)若点![]() ,求椭圆的方程及△ABC的面积;
,求椭圆的方程及△ABC的面积;
(2)若![]() 为动点,设直线
为动点,设直线![]() 与
与![]() 的斜率分别为
的斜率分别为![]() 、
、![]() .
.
①试问![]() 是否为定值?若为定值,请求出;否则,请说明理由;
是否为定值?若为定值,请求出;否则,请说明理由;
②求△AEF的面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,椭圆
中,椭圆![]() 的离心率为
的离心率为![]() ,右顶点为
,右顶点为![]() ,直线
,直线![]() 过原点
过原点![]() ,且点
,且点![]() 在x轴的上方,直线
在x轴的上方,直线![]() 与
与![]() 分别交直线
分别交直线![]() :
:![]() 于点
于点![]() 、
、![]() .
.
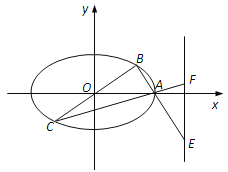
(1)若点![]() ,求椭圆的方程及△ABC的面积;
,求椭圆的方程及△ABC的面积;
(2)若![]() 为动点,设直线
为动点,设直线![]() 与
与![]() 的斜率分别为
的斜率分别为![]() 、
、![]() .
.
①试问![]() 是否为定值?若为定值,请求出;否则,请说明理由;
是否为定值?若为定值,请求出;否则,请说明理由;
②求△AEF的面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
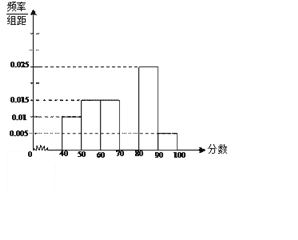
【题目】某校从参加考试的学生中抽出60名学生,将其成绩(均为整数)分成六组[40,50),[50,60) ...[90,100]后,画出如下部分频率分布直方图.观察图形的信息,回答下列问题:
(Ⅰ) 求成绩落在[70,80)上的频率,并补全这个频率分布直方图;
(Ⅱ) 估计这次考试的及格率(60分及以上为及格)和平均分;
(Ⅲ) 设学生甲、乙的成绩属于区间[40,50),现从成绩属于该区间的学生中任选两人,求甲、乙中至少有一人被选的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】刘老师是一位经验丰富的高三理科班班主任,经长期研究,他发现高中理科班的学生的数学成绩(总分150分)与理综成绩(物理、化学与生物的综合,总分300分)具有较强的线性相关性,以下是刘老师随机选取的八名学生在高考中的数学得分x与理综得分y(如下表):
学生编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
数学分数x | 52 | 64 | 87 | 96 | 105 | 123 | 132 | 141 |
理综分数y | 112 | 132 | 177 | 190 | 218 | 239 | 257 | 275 |
参考数据及公式: ![]() .
.
(1)求出y关于x的线性回归方程;
(2)若小汪高考数学110分,请你预测他理综得分约为多少分?(精确到整数位);
(3)小金同学的文科一般,语文与英语一起能稳定在215分左右.如果他的目标是在
高考总分冲击600分,请你帮他估算他的数学与理综大约分别至少需要拿到多少分?(精确到整数位).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com