
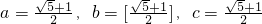 给出下列结论:(1)2lnb=lna+lnc(2)ln2b=lnalnc;(3)lna+lnb+lnc=0(4)lnalnblnc=1(5)lna+lnb+lnc=1.其中正确的结论是________.
给出下列结论:(1)2lnb=lna+lnc(2)ln2b=lnalnc;(3)lna+lnb+lnc=0(4)lnalnblnc=1(5)lna+lnb+lnc=1.其中正确的结论是________. ,
,
 ,所以①对;
,所以①对; ,
, ,然后代入各个选项,判断出它们的对错即可.
,然后代入各个选项,判断出它们的对错即可.

科目:高中数学 来源: 题型:
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| A、是等差数列但不是等比数列 |
| B、是等比数列但不是等差数列 |
| C、既是等差数列又是等比数列 |
| D、既不是等差数列也不是等比数列 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源:新课标高三数学等比数列、数列通项的求法专项训练(河北) 题型:单选题
设x∈R,记不超过x的最大整数为[x],令{x}=x-[x],则,,( )
| A.是等差数列但不是等比数列 |
| B.是等比数列但不是等差数列 |
| C.既是等差数列又是等比数列 |
| D.既不是等差数列也不是等比数列 |
查看答案和解析>>
科目:高中数学 来源:2011年广东省广州市仲元中学高三数学专题训练:数列(解析版) 题型:选择题
 },[
},[ ],
], ( )
( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com