
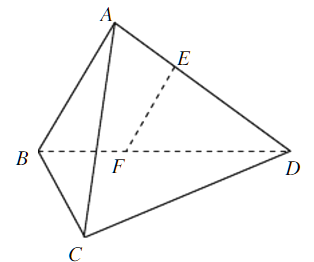
【题目】如图,在三棱锥A-BCD中,AB⊥AD,BC⊥BD,平面ABD⊥平面BCD,点E、F(E与A、D不重合)分别在棱AD,BD上,且EF⊥AD.
求证:(1)EF∥平面ABC;
(2)AD⊥AC.
科目:高中数学 来源: 题型:
【题目】拖延症总是表现在各种小事上,但日积月累,特别影响个人发展.某校的一个社会实践调查小组,在对该校学生进行“是否有明显拖延症”的调查中,随机发放了110份问卷.对收回的100份有效问卷进行统计,得到如下![]() 列联表:
列联表:
有明显拖延症 | 无明显拖延症 | 合计 | |
男 | 35 | 25 | 60 |
女 | 30 | 10 | 40 |
合计 | 65 | 35 | 100 |
(Ⅰ)按女生是否有明显拖延症进行分层,已经从40份女生问卷中抽取了8份问卷,现从这8份问卷中再随机抽取3份,并记其中无明显拖延症的问卷的份数为![]() ,试求随机变量
,试求随机变量![]() 的分布列和数学期望;
的分布列和数学期望;
(Ⅱ)若在犯错误的概率不超过![]() 的前提下认为无明显拖延症与性别有关,那么根据临界值表,最精确的
的前提下认为无明显拖延症与性别有关,那么根据临界值表,最精确的![]() 的值应为多少?请说明理由.
的值应为多少?请说明理由.
附:独立性检验统计量 ,其中
,其中![]() .
.
独立性检验临界值表:
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】a,b为空间中两条互相垂直的直线,等腰直角三角形ABC的直角边AC所在直线与a,b都垂直,斜边AB以直线AC为旋转轴旋转,有下列结论:
①当直线AB与a成60°角时,AB与b成30°角;
②当直线AB与a成60°角时,AB与b成60°角;
③直线AB与a所称角的最小值为45°;
④直线AB与a所称角的最小值为60°;
其中正确的是________。(填写所有正确结论的编号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}满足:a4=7,a10=19,其前n项和为Sn .
(1)求数列{an}的通项公式an及Sn;
(2)若等比数列{bn}的前n项和为Tn , 且b1=2,b4=S4 , 求Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面内给定三个向量 ![]() =(3,2),
=(3,2), ![]() =(﹣1,2),
=(﹣1,2), ![]() =(4,1).回答下列问题:
=(4,1).回答下列问题:
(1)若( ![]() +k
+k ![]() )∥(2
)∥(2 ![]() ﹣
﹣ ![]() ),求实数k;
),求实数k;
(2)设 ![]() =(x,y)满足(
=(x,y)满足( ![]() ﹣
﹣ ![]() )∥(
)∥( ![]() +
+ ![]() )且|
)且| ![]() ﹣
﹣ ![]() |=1,求
|=1,求 ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() (
(![]() )的上、下两个焦点分别为
)的上、下两个焦点分别为![]() ,
, ![]() ,过
,过![]() 的直线交椭圆于
的直线交椭圆于![]() ,
, ![]() 两点,且
两点,且![]() 的周长为8,椭圆
的周长为8,椭圆![]() 的离心率为
的离心率为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)已知![]() 为坐标原点,直线
为坐标原点,直线![]() :
: ![]() 与椭圆
与椭圆![]() 有且仅有一个公共点,点
有且仅有一个公共点,点![]() ,
, ![]() 是直线
是直线![]() 上的两点,且
上的两点,且![]() ,
, ![]() ,求四边形
,求四边形![]() 面积
面积![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com