
【题目】设 ![]() 表示三条不同的直线,
表示三条不同的直线, ![]() 表示三个不同的平面,给出下列三个命题:①若
表示三个不同的平面,给出下列三个命题:①若 ![]() ,则
,则 ![]() ;②若
;②若 ![]() ,
, ![]() 是
是 ![]() 在
在 ![]() 内的射影,
内的射影, ![]() ,则
,则 ![]() ;③若
;③若 ![]() 则
则 ![]() . 其中真命题的个数为( )
. 其中真命题的个数为( )
A.0
B.1
C.2
D.3
科目:高中数学 来源: 题型:
【题目】已知命题p:对数 ![]() 有意义;命题q:实数t满足不等式
有意义;命题q:实数t满足不等式 ![]() .(Ⅰ)若命题p为真,求实数
.(Ⅰ)若命题p为真,求实数 ![]() 的取值范围;
的取值范围;
(Ⅱ)若命题p是命题q的充分不必要条件,求实数 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某初级中学有三个年级,各年级男、女人数如下表:
初一年级 | 初二年级 | 初三年级 | |
女生 | 370 |
| 200 |
男生 | 380 | 370 | 300 |
已知在全校学生中随机抽取1名,抽到初二年级女生的概率是0.19.
(1)求 ![]() 的值;
的值;
(2)用分层抽样的方法在初三年级中抽取一个容量为5的样本,求该样本中女生的人数;
(3)用随机抽样的方法从初二年级女生中选出8人,测量它们的左眼视力,结果如下:1.2,1.5,1.2,1.5,1.5,1.3,1.0,1.2.把这8人的左眼视力看作一个总体,从中任取一个数,求该数与样本平均数之差的绝对值不超过0.1的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax3-3x2+1,若f(x)存在唯一的零点x0,且x0>0,则a的取值范围是( )
A.(2,+∞)
B.(1,+∞)
C.(-∞,-2)
D.(-∞,-1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学著作《九章算术》有如下问题:“今有蒲(水生植物名)生一日,长三尺;莞(植物名,俗称水葱、席子草)生一日,长一尺.蒲生日自半,莞生日自倍.问几何日而长等?”意思是:今有蒲生长1日,长为3尺;莞生长1日,长为1尺.蒲的生长逐日减半,莞的生长逐日增加1倍.若蒲、莞长度相等,则所需的时间约为日.(结果保留一位小数,参考数据:lg2≈0.30,lg3≈0.48)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列![]() 中,若对任意
中,若对任意![]() 都有
都有![]() (
(![]() 为常数)成立,则称
为常数)成立,则称![]() 为“等差比数列”,下面对“等差比数列” 的判断:①
为“等差比数列”,下面对“等差比数列” 的判断:①![]() 不可能为
不可能为![]() ;②等差数列一定是等差比数列; ③等比数列一定是等差比数列 ;④通项公式为
;②等差数列一定是等差比数列; ③等比数列一定是等差比数列 ;④通项公式为![]() (其中
(其中![]() ,且
,且![]() ,
,![]() )的数列一定是等差比数列,其中正确的判断是( )
)的数列一定是等差比数列,其中正确的判断是( )
A. ①③④ B. ②③④ C. ①④ D. ①③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆 ![]() :
: ![]() (其中
(其中 ![]() 为圆心)上的每一点横坐标不变,纵坐标变为原来的一半,得到曲线
为圆心)上的每一点横坐标不变,纵坐标变为原来的一半,得到曲线 ![]() .
.
(1)求曲线 ![]() 的方程;
的方程;
(2)若点 ![]() 为曲线
为曲线 ![]() 上一点,过点
上一点,过点 ![]() 作曲线
作曲线 ![]() 的切线交圆
的切线交圆 ![]() 于不同的两点
于不同的两点 ![]() (其中
(其中 ![]() 在
在 ![]() 的右侧),已知点
的右侧),已知点 ![]() .求四边形
.求四边形 ![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个正方体的平面展开图及该正方体的直观图的示意图如图所示.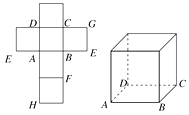
(1)请按字母F、G、H标记在正方体相应地顶点处(不需要说明理由);
(2)判断平面BEG与平面ACH的位置关系.并说明你的结论;
(3)证明:直线DF⊥平面BEG.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从装有 2个红球和 2个白球的口袋中任取 2个球,则下列每对事件中,互斥事件的对数是( )对
(1)“至少有 1个白球”与“都是白球” (2)“至少有 1个白球”与“至少有 1个红球”
(3)“至少有 1个白球”与“恰有 2个白球” (4)“至少有 1个白球”与“都是红球”
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com