
【题目】已知数列{an}的前n项和Sn , 且Sn=2n2+3n;
(1)求它的通项an .
(2)若bn= ![]() ,求数列{bn}的前n项和Tn .
,求数列{bn}的前n项和Tn .
【答案】
(1)解:由Sn=2n2+3n,
当n=1时,a1=S1=5;
当n>1时,an=Sn﹣Sn﹣1=2n2+3n﹣2(n﹣1)2﹣3(n﹣1)
=4n+1,对n=1也成立.
则通项an=4n+1;
(2)解:bn= ![]() =
= ![]() =
= ![]() (
( ![]() ﹣
﹣ ![]() ),
),
即有前n项和Tn= ![]() (
( ![]() ﹣
﹣ ![]() +
+ ![]() ﹣
﹣ ![]() +…+
+…+ ![]() ﹣
﹣ ![]() )
)
= ![]() (
( ![]() ﹣
﹣ ![]() )=
)= ![]() .
.
【解析】(1)由数列的通项和求和的关系:当n=1时,a1=S1 , 当n>1时,an=Sn﹣Sn﹣1 , 化简即可得到所求通项;(2)求得bn= ![]() =
= ![]() =
= ![]() (
( ![]() ﹣
﹣ ![]() ),再由数列的求和方法:裂项相消求和,化简整理即可得到所求和.
),再由数列的求和方法:裂项相消求和,化简整理即可得到所求和.
【考点精析】通过灵活运用数列的前n项和和等差数列的性质,掌握数列{an}的前n项和sn与通项an的关系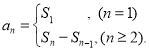 ;在等差数列{an}中,从第2项起,每一项是它相邻二项的等差中项;相隔等距离的项组成的数列是等差数列即可以解答此题.
;在等差数列{an}中,从第2项起,每一项是它相邻二项的等差中项;相隔等距离的项组成的数列是等差数列即可以解答此题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知集合M={x|﹣2<x<2},N={x|x2﹣2x﹣3<0},则集合M∩N=( )
A.{x|x<﹣2}
B.{x|x>3}
C.{x|﹣1<x<2}
D.{x|2<x<3}
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某农场预算用5600元购买单价为50元(每吨)的钾肥和20元(每吨)的氮肥,希望使两种肥料的总数量(吨)尽可能的多,但氮肥数不少于钾肥数,且不多于钾肥数的1.5倍.
(Ⅰ)设买钾肥x吨,买氮肥y吨,按题意列出约束条件、画出可行域,并求钾肥、氮肥各买多少才行?
(Ⅱ)已知A(10,0),O是坐标原点,P(x,y)在(Ⅰ)中的可行域内,求  的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱柱ABCD﹣A1B1C1D1的底面ABCD是平行四边形,且AB=1,BC=2,∠ABC=60°,E为BC的中点,AA1⊥平面ABCD. (Ⅰ)证明:平面A1AE⊥平面A1DE;
(Ⅱ)若DE=A1E,试求二面角E﹣A1C﹣D的余弦值.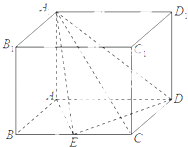
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列所给4个图象中,与所给3件事吻合最好的顺序为( )
(1)小明离开家不久,发现自己把作业本忘在家里了,于是立刻返回家里取了作业本再上学;
(2)小明骑着车一路以常速行驶,只是在途中遇到一次交通堵塞,耽搁了一些时间;
(3)小明出发后,心情轻松,缓缓行进,后来为了赶时间开始加速.
A.(4)(1)(2)
B.(4)(2)(3)
C.(4)(1)(3)
D.(1)(2)(4)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数f(x),若a,b,c∈R,f(a),f(b),f(c)为某一三角形的三边长,则称f(x)为“可构造三角形函数”,已知函数f(x)= ![]() 是“可构造三角形函数”,则实数t的取值范围是( )
是“可构造三角形函数”,则实数t的取值范围是( )
A.[0,+∞)
B.[0,1]
C.[1,2]
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com