
【题目】如图C,D是以AB为直径的圆上的两点,![]() ,F是AB上的一点,且
,F是AB上的一点,且![]() ,将圆沿AB折起,使点C在平面ABD的射影E在BD上,已知
,将圆沿AB折起,使点C在平面ABD的射影E在BD上,已知![]()

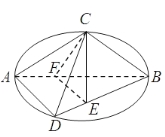
(1)求证:AD![]() 平面BCE
平面BCE
(2)求证:AD//平面CEF;
(3)求三棱锥A-CFD的体积.
【答案】(1)参考解析;(2)参考解析;(3) ![]()
【解析】
试题分析:(1)因为由于AB是圆的直径,所以AD⊥BD,又因为点C在平面ABD的射影E在BD上,所以CE⊥平面ADB.又因为![]() 平面ADB.所以AD⊥CE.又因为
平面ADB.所以AD⊥CE.又因为![]() .所以AD⊥平面BCE.
.所以AD⊥平面BCE.
(2)因为![]() ,
,![]() .有直角三角形的勾股定理可得
.有直角三角形的勾股定理可得![]() .在直角三角形BCE中,又
.在直角三角形BCE中,又![]() .所以
.所以![]() .又BD=3,
.又BD=3,![]() .所以可得
.所以可得![]() .所以AD∥FE,又因为
.所以AD∥FE,又因为![]() 平面CEF,
平面CEF,![]() 平面CE.所以AD//平面CEF.
平面CE.所以AD//平面CEF.
(3)通过转换顶点三棱锥A-CFD的体积![]() .因为
.因为![]()
![]() .所以
.所以![]() .
.
试题解析:(1)证明:依题意:![]()
![]()
![]()
![]() 平面
平面![]() ∴
∴![]()
![]()
![]()
![]()
![]() ∴
∴![]() 平面
平面![]() . 4分
. 4分
(2)证明:![]() 中,
中,![]() ,
,![]() ∴
∴![]()
![]() 中,
中,![]() ,
,![]() ∴
∴![]() .
.
∴![]() . ∴
. ∴![]()
![]()
![]() 在平面
在平面![]() 外,
外,![]() 在平面
在平面![]() 内,
内,
∴![]() 平面
平面![]() . 8分
. 8分
(3)解:由(2)知![]() ,
,![]()
![]() ,且
,且![]()
![]()
![]() 平面
平面![]()
∴![]() . 12分
. 12分


科目:高中数学 来源: 题型:
【题目】设F为双曲线 ![]() ﹣
﹣ ![]() =1(a>b>0)的右焦点,过点F的直线分别交两条渐近线于A,B两点,OA⊥AB,若2|AB|=|OA|+|OB|,则该双曲线的离心率为( )
=1(a>b>0)的右焦点,过点F的直线分别交两条渐近线于A,B两点,OA⊥AB,若2|AB|=|OA|+|OB|,则该双曲线的离心率为( ) 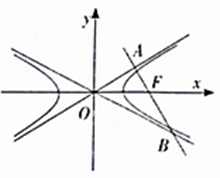
A.![]()
B.2
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知:函数f(x)= ![]() (a>0且a≠1).
(a>0且a≠1).
(Ⅰ)求函数f(x)的定义域;
(Ⅱ)判断函数f(x)的奇偶性,并加以证明;
(Ⅲ)设a=![]() ,解不等式f(x)>0.
,解不等式f(x)>0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() ∈[1,+∞).
∈[1,+∞).
(1)当![]() 时,判断函数
时,判断函数![]() 的单调性并证明;
的单调性并证明;
(2)当![]() 时,求函数
时,求函数![]() 的最小值;
的最小值;
(3)若对任意![]() ∈[1,+∞),
∈[1,+∞),![]() >0恒成立,试求实数
>0恒成立,试求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设命题p:函数y=sin2x的最小正周期为 ![]() ;命题q:函数y=cosx的图象关于直线x=
;命题q:函数y=cosx的图象关于直线x= ![]() 对称.则下列判断正确的是( )
对称.则下列判断正确的是( )
A.p为真
B.¬q为假
C.p∧q为假
D.p∨q为真
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校某研究性学习小组在对学生上课注意力集中情况的调查研究中,发现其在40分钟的一节课中,注意力指数y与听课时间x(单位:分钟)之间的关系满足如图所示的图象,当x∈(0,12]时,图象是二次函数图象的一部分,其中顶点A(10,80),过点B(12,78);当x∈[12,40]时,图象是线段BC,其中C(40,50).根据专家研究,当注意力指数大于62时,学习效果最佳.
(1)试求y=f(x)的函数关系式;
(2)教师在什么时段内安排内核心内容,能使得学生学习效果最佳?请说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正方体ABCD﹣A1B1C1D1中,E、F分别是BB1、CD的中点.
(1)求证:平面AED⊥平面A1FD1;
(2)在AE上求一点M,使得A1M⊥平面ADE.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx,g(x)=f(x)+ax2+bx,其中函数g(x)的图象在点(1,g(1))处的切线平行于x轴.
(1)确定a与b的关系;
(2)若a≥0,试讨论函数g(x)的单调性.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥S﹣ABCD中,△ABD是正三角形,CB=CD,SC⊥BD. 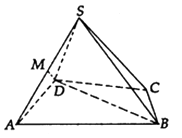
(1)求证:SA⊥BD;
(2)若∠BCD=120°,M为棱SA的中点,求证:DM∥平面SBC.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com