
【题目】如图,长方体![]() 的长,宽,高分别为4,3,5,现有一甲壳虫从
的长,宽,高分别为4,3,5,现有一甲壳虫从![]() 点出发沿长方体表面爬行到
点出发沿长方体表面爬行到![]() 点来获取食物.
点来获取食物.
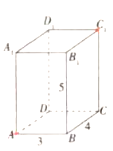
(1)甲壳虫想尽快获取食物可通过哪些路径获取?
(2)哪条获取食物的路径最短?最短为多少?
(3)此类问题的一般处理方法是什么?
【答案】(1)见解析 (2)第②种方案使得爬行路程最短,最短路程为![]() .(3)见解析
.(3)见解析
【解析】
(1)即求长方体表面上从![]() 点到
点到![]() 点的距离最短,把长方体剪开再展开,转化为平面上两点之间线段最短,分类讨论求出展开图中线段
点的距离最短,把长方体剪开再展开,转化为平面上两点之间线段最短,分类讨论求出展开图中线段![]() 的长,即可求出结论;
的长,即可求出结论;
(2)比较(1)中的长度,即可求解;
(3)表面上两点距离最小,利用展开图,转化为平面上两点距离最小值的问题.
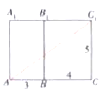
(1).①将平面![]() 与平面
与平面![]() ,展开放在同一平面内,
,展开放在同一平面内,
如图(1),可求出此时的最短距离![]() ;
;
②将平面![]() 与平面
与平面![]() 展开放在同一平面内,
展开放在同一平面内,
如图(2),可求出此时的最短距离![]() ;
;
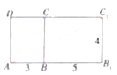
③将平面![]() 与平面
与平面![]() 展开放在同一平面内,
展开放在同一平面内,
如图(3),可求出此时的最短距离![]() .
.

(2):由(1)知![]() ,
,
所以第②种方案使得爬行路程最短,最短路程为![]() .
.
(3)表面上两点最小,通常把长方体按一定的方式展开即可求解.


科目:高中数学 来源: 题型:
【题目】将![]() 方格纸中每个小方格染三种颜色之一,使得每种颜色的小方格的个数相等.若相邻两个小方格的颜色不同,称他们的公共边为“分割边”,则分割边条数的最小值为( )
方格纸中每个小方格染三种颜色之一,使得每种颜色的小方格的个数相等.若相邻两个小方格的颜色不同,称他们的公共边为“分割边”,则分割边条数的最小值为( )
A.33B.56C.64D.78
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)如果把棱柱中过不相邻的两条侧棱的截面叫棱柱的“对角面”,则平行六面体的对角面的形状是_______,直平行六面体的对角面的形状是______;
(2)过正三棱柱底面的一边和两底面中心连线段的中点作截面,则这个截面的形状为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形.平面ABC⊥平面AA1C1C,AB=3,BC=5.

(Ⅰ)求证:AA1⊥平面ABC;
(Ⅱ)求二面角A1-BC1-B1的余弦值;
(Ⅲ)证明:在线段BC1存在点D,使得AD⊥A1B,并求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列![]() 的前
的前![]() 项的和为
项的和为![]() 且
且![]() 数列
数列![]() 满足
满足![]() 且对任意正整数
且对任意正整数![]() 都有
都有![]() 成等比数列.
成等比数列.
(1)求数列![]() 的通项公式.
的通项公式.
(2)证明数列![]() 为等差数列.
为等差数列.
(3)令![]() 问是否存在正整数
问是否存在正整数![]() 使得
使得![]() 成等比数列?若存在,求出
成等比数列?若存在,求出![]() 的值,若不存在,说明理由.
的值,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有一段“三段论”,其推理是这样的:对于可导函数![]() ,若
,若![]() ,则
,则![]() 是函数
是函数![]() 的极值点,因为函数
的极值点,因为函数![]() 满足
满足![]() ,所以
,所以![]() 是函数
是函数![]() 的极值点”,结论以上推理
的极值点”,结论以上推理![]()
![]()
A. 大前提错误B. 小前提错误C. 推理形式错误D. 没有错误
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com