
|
| a |
|
|
| x2 |
| 4 |
|
|
|
|
| x2 |
| 4 |
| |2cosθ+2sinθ| | ||
|
2
| ||||
|
| π |
| 4 |
2
| ||
| 5 |


 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:高中数学 来源: 题型:
|
| a |
|
|
| x2 |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•江苏二模)选做题
(2012•江苏二模)选做题| PC |
| PA |
| BD |
| DC |
|
| x2 |
| 16 |
| y2 |
| 9 |
| 13 |
| 4 |
查看答案和解析>>
科目:高中数学 来源:2010年江苏省扬州中学高三第四次模拟考试数学试题 题型:解答题
[选做题]
A.选修4—1:几何证明选讲
如图,设AB为⊙O的任一条不与直线l垂直的直径,P是⊙O与l的公共点,AC⊥l,BD⊥l,垂足分别为C,D,且PC=PD,求证:
(1)l是⊙O的切线;
(2)PB平分∠ABD.
|
 对应的变换将点
对应的变换将点 与
与 分别变换成点
分别变换成点 与
与 .求矩阵
.求矩阵 ;
; 的最大值.
的最大值.查看答案和解析>>
科目:高中数学 来源:2010-2011学年江苏省徐州市沛县湖西中学高三(上)期末数学模拟试卷(解析版) 题型:解答题
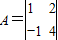 ,向量
,向量 =
= .
. (t为参数),P是椭圆
(t为参数),P是椭圆 上任意一点,求点P到直线l的距离的最大值.
上任意一点,求点P到直线l的距离的最大值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com