
【题目】某工厂生产一种仪器的元件,由于受生产能力和技术水平等因素的限制,会产生一些次品,根据经验知道,次品数P(万件)与日产量x(万件)之间满足关系: 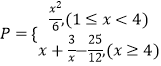 已知每生产l万件合格的元件可以盈利2万元,但每生产l万件次品将亏损1万元.(利润=盈利一亏损)
已知每生产l万件合格的元件可以盈利2万元,但每生产l万件次品将亏损1万元.(利润=盈利一亏损)
(1)试将该工厂每天生产这种元件所获得的利润T(万元)表示为日产量x(万件)的函数;
(2)当工厂将这种仪器的元件的日产量x定为多少时获得的利润最大,最大利润为多少?
【答案】
(1)解:当1≤x<4时,合格的元件数为 ![]() ,
,
利润 ![]() ;
;
当x≥4时,合格的元件数为 ![]() ,
,
利润 ![]() ,
,
综上,该工厂每天生产这种元件所获得的利润 
(2)解:当1≤x<4时, ![]() ,对称轴x=2,此时利润T的最大值Tmax=T(2)=2.
,对称轴x=2,此时利润T的最大值Tmax=T(2)=2.
当x≥4时, ![]() ,
,
所以 ![]() 在[4,+∞)上是减函数,
在[4,+∞)上是减函数,
此时利润T的最大值Tmax=T(4)=0,
综上所述,当x=2时,T取最大值2,
即当日产量定为2(万件)时,工厂可获得最大利润2万元.
【解析】(1)由已知中次数数P(万件)与日产量x(万件)之间的关系式,可求出合格的元件数,进而根据每生产l万件合格的元件可以盈利2万元,但每生产l万件次品将亏损1万元,得到利润T(万元)用日产量x(万件)的函数解析式.(2)由(1)中结论,结合二次函数的图象和性质,可以求出日产量x定为多少时获得的利润最大,及最大利润值


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:高中数学 来源: 题型:
【题目】已知y=f(x)是R上的可导函数,对于任意的正实数t,都有函数g(x)=f(x+t)﹣f(x)在其定义域内为减函数,则函数y=f(x)的图象可能为如图中( )
A.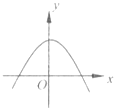
B.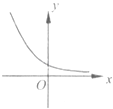
C.
D.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l:ax﹣y+1=0与x轴,y轴分别交于点A,B.
(1)若a>0,点M(1,﹣1),点N(1,4),且以MN为直径的圆过点A,求以AN为直径的圆的方程;
(2)以线段AB为边在第一象限作等边三角形ABC,若a=﹣ ![]() ,且点P(m,
,且点P(m, ![]() )(m>0)满足△ABC与△ABP的面积相等,求m的值.
)(m>0)满足△ABC与△ABP的面积相等,求m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量![]() ,
,![]() ,函数
,函数![]() 的最大值为
的最大值为![]() .
.

(1)求![]() 的大小;
的大小;
(2)将函数![]() 的图象向左平移
的图象向左平移![]() 个单位,再将所得图象上各点的横坐标缩短为原来的
个单位,再将所得图象上各点的横坐标缩短为原来的![]() ,纵坐标不变,得到函数
,纵坐标不变,得到函数![]() 的图象,作出函数
的图象,作出函数![]() 在
在![]() 的图象.
的图象.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正方体ABCD﹣A1B1C1D1中,E是棱CC1的中点,F是侧面BCC1B1内的动点,且A1F∥平面D1AE,则A1F与平面BCC1B1所成角的正切值t构成的集合是( ) 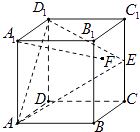
A.{t| ![]() }
}
B.{t| ![]() ≤t≤2}
≤t≤2}
C.{t|2 ![]() }
}
D.{t|2 ![]() }
}
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A(4,﹣3),B(2,﹣1)和直线l:4x+3y﹣2=0.
(1)求在直角坐标平面内满足|PA|=|PB|的点P的方程;
(2)求在直角坐标平面内一点P满足|PA|=|PB|且点P到直线l的距离为2的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】假设关于某设备的使用年限x(年)和所支出的维修费用y(万元)有如下的统计资料:
x | 2 | 3 | 4 | 5 | 6 |
y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
(1)画出散点图并判断是否线性相关;
(2)如果线性相关,求线性回归方程;
(3)估计使用年限为10年时,维修费用是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com