
【题目】已知函数![]() .
.
(Ⅰ)求函数![]() 的单调区间;
的单调区间;
(Ⅱ)若函数![]() 上是减函数,求实数a的最小值;
上是减函数,求实数a的最小值;
(Ⅲ)若![]() ,使
,使![]() (
(![]() )成立,求实数a的取值范围.
)成立,求实数a的取值范围.
【答案】(1) 单调减区间是![]() ,增区间是
,增区间是![]() ;(2)
;(2)![]() ; (3)
; (3)![]() .
.
【解析】
试题(1) 根据原函数在区间上的单调递减转化为导数在该区间内小于等于零恒成立,再把恒成立转化为最值求解,在求解的过程中利用了二次三项式的配方;(2)命题的等价变换是解决本小题的关键,“若![]() 使
使![]() 成立”等价于 “当
成立”等价于 “当![]() 时,有
时,有![]() ”,于是整个问题就化为求函数的最值,然后利用导数分析单调性,进而求最值。
”,于是整个问题就化为求函数的最值,然后利用导数分析单调性,进而求最值。
试题解析:由已知函数![]() 的定义域均为
的定义域均为![]() ,且
,且![]() .
.
(1)函数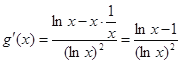 , 2分
, 2分
因f(x)在![]() 上为减函数,故
上为减函数,故![]() 在
在![]() 上恒成立.
上恒成立.
所以当![]() 时,
时,![]() .
.
又![]()
![]() ,
,
故当![]() ,即
,即![]() 时,
时,![]() .
.
所以![]() 于是
于是![]() ,故a的最小值为
,故a的最小值为![]() . 6分
. 6分
(2)命题“若![]() 使
使![]() 成立”等价于 “当
成立”等价于 “当![]() 时,有
时,有![]() ”.
”.
由(Ⅱ),当![]() 时,
时,![]() ,
,![]()
![]() .
.
问题等价于:“当![]() 时,有
时,有![]() ”. 8分
”. 8分
![]() 当
当![]() 时,由(Ⅱ),
时,由(Ⅱ),![]() 在
在![]() 上为减函数,
上为减函数,
则![]() =
=![]() ,故
,故![]() . 10分
. 10分
![]() 当
当![]() 时,由于
时,由于![]()
![]() 在
在![]() 上为增函数,
上为增函数,
故![]() 的值域为
的值域为![]() ,即
,即![]() .
.
由![]() 的单调性和值域知,
的单调性和值域知,![]() 唯一
唯一![]() ,使
,使![]() ,且满足:
,且满足:
当![]() 时,
时,![]() ,
,![]() 为减函数;
为减函数;
当![]() 时,
时,![]() ,
,![]() 为增函数;
为增函数;
所以,![]() =
=![]() ,
,![]() .
.
所以,![]() ,与
,与![]() 矛盾,不合题意. 11分
矛盾,不合题意. 11分
综上,得![]() . 12分
. 12分


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】下表是某地某年月平均气温(华氏度):
月份 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
平均气温 | 21.4 | 26.0 | 36.0 | 48.8 | 59.1 | 68.6 | 73.0 | 71.9 | 64.7 | 53.5 | 39.8 | 27.7 |
以月份为x轴(![]() 月份
月份![]() ),以平均气温为y轴.
),以平均气温为y轴.
(1)用正弦曲线去拟合这些数据;
(2)估计这个正弦曲线的周期T和振幅A;
(3)下面三个函数模型中,哪一个最适合这些数据?
①![]() ;②
;②![]() ;③
;③![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题正确的个数是:( )
①对于两个分类变量![]() 与
与![]() 的随机变量
的随机变量![]() 的观测值
的观测值![]() 来说,
来说,![]() 越小,判断“
越小,判断“![]() 与
与![]() 有关系”的把握程度越大;
有关系”的把握程度越大;
②在相关关系中,若用![]() 拟合时的相关指数为
拟合时的相关指数为![]() ,用
,用![]() 拟合时的相关指数为
拟合时的相关指数为![]() ,且
,且![]() ,则
,则![]() 的拟合效果好;
的拟合效果好;
③利用计算机产生![]() 之间的均匀随机数
之间的均匀随机数![]() ,则事件“
,则事件“![]() ”发生的概率为
”发生的概率为![]() ;
;
④“![]() ”是“
”是“![]() ”的充分不必要条件
”的充分不必要条件
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 的极坐标方程是
的极坐标方程是![]() ,以极点为平面直角坐标系的原点,极轴为
,以极点为平面直角坐标系的原点,极轴为![]() 轴的正半轴,且取相等的单位长度,建立平面直角坐标系,直线
轴的正半轴,且取相等的单位长度,建立平面直角坐标系,直线![]() 的参数方程是
的参数方程是 (
(![]() 是参数),设点
是参数),设点![]() .
.
(Ⅰ)将曲线![]() 的极坐标方程化为直角坐标方程,将直线
的极坐标方程化为直角坐标方程,将直线![]() 的参数方程化为普通方程;
的参数方程化为普通方程;
(Ⅱ)设直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产甲,乙两种图画纸,计划每种图画纸的生产量不少于8t,已知生产甲种图画纸1t要用芦苇7t、黄麻3t、枫树5t;生产乙种图画纸1t要用芦苇3t、黄麻4t、枫树8 t.现在仓库内有芦苇300t、黄麻150t.枫树200t,试列出满足题意的不等式组.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一半径为![]() 的水轮,水轮圆心
的水轮,水轮圆心![]() 距离水面2
距离水面2![]() ,已知水轮每分钟转动(按逆时针方向)3圈,当水轮上点
,已知水轮每分钟转动(按逆时针方向)3圈,当水轮上点![]() 从水中浮现时开始计时,即从图中点
从水中浮现时开始计时,即从图中点![]() 开始计算时间.
开始计算时间.
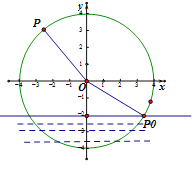
(1)当![]() 秒时点
秒时点![]() 离水面的高度_________;
离水面的高度_________;
(2)将点![]() 距离水面的高度
距离水面的高度![]() (单位:
(单位: ![]() )表示为时间
)表示为时间![]() (单位:
(单位: ![]() )的函数,则此函数表达式为_______________ .
)的函数,则此函数表达式为_______________ .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com