
函数 的定义域为
的定义域为 ,若存在闭区间
,若存在闭区间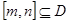 ,使得函数
,使得函数 满足以下两个条件:(1)
满足以下两个条件:(1) 在[m,n]上是单调函数;(2)
在[m,n]上是单调函数;(2)  在[m,n]上的值域为[2m,2n],则称区间[m,n]为
在[m,n]上的值域为[2m,2n],则称区间[m,n]为 的“倍值区间”.下列函数中存在“倍值区间”的有 (填上所有正确的序号)
的“倍值区间”.下列函数中存在“倍值区间”的有 (填上所有正确的序号)
① =x2(x≥0); ②
=x2(x≥0); ② =ex(x∈R);
=ex(x∈R);
③ =
= ;④
;④ =
=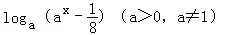 .
.
①③④
解析试题分析:函数中存在“倍值区间”,则:(1) 在
在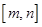 内是单调函数;(2)
内是单调函数;(2) ,或
,或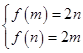 ,①
,①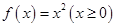 ,若存在“倍值区间”
,若存在“倍值区间” 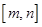 ,则
,则 ,∴
,∴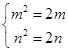 ,∴
,∴ ,∴
,∴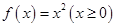 ,故存在“倍值区间”
,故存在“倍值区间”  ;②
;②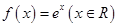 ,若存在“倍值区间”
,若存在“倍值区间” 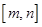 ,则
,则 ,∴
,∴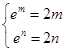 ,构建函数
,构建函数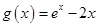 ,∴
,∴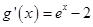 ,∴函数在
,∴函数在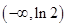 上单调减,在
上单调减,在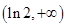 上单调增,∴函数在
上单调增,∴函数在 处取得极小值,且为最小值, ∵
处取得极小值,且为最小值, ∵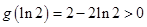 ,∴
,∴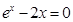 无解,故函数不存在“倍值区间”;
无解,故函数不存在“倍值区间”;
③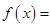
 ,
, ,若存在“倍值区间”
,若存在“倍值区间” 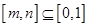 ,
,
则 ,∴
,∴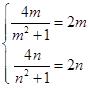 ,∴
,∴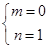 ,故存在“倍值区间”
,故存在“倍值区间” 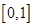 ;④
;④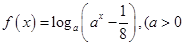 且
且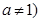 ,不妨设
,不妨设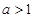 ,则函数在定义域内为单调增函数,若存在“倍值区间”
,则函数在定义域内为单调增函数,若存在“倍值区间” 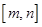 ,则
,则 ,∴
,∴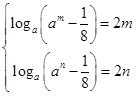 ,则方程
,则方程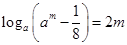 ,即
,即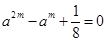 ,由于该方程有两个不等的正根,故存在“倍值区间”
,由于该方程有两个不等的正根,故存在“倍值区间” 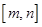 ;综上知,所给函数中存在“倍值区间”的有①③④,故答案为:①③④.
;综上知,所给函数中存在“倍值区间”的有①③④,故答案为:①③④.
考点:函数的值域;命题的真假判断与应用.


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com