
【题目】从甲袋内摸出1个红球的概率是![]() ,从乙袋内摸出1个红球的概率是
,从乙袋内摸出1个红球的概率是![]() ,从两袋内各摸出1个球,则
,从两袋内各摸出1个球,则![]() 等于( )
等于( )
A. 2个球不都是红球的概率B. 2个球都是红球的概率
C. 至少有1个红球的概率D. 2个球中恰好有1个红球的概率
【答案】C
【解析】
根据题意,易得从甲袋中摸出的球不是红球与从乙袋中摸出的球不是红球的概率,进而以此分析选项:对于A,2个球都不是红球,即从甲袋中摸出的球不是红球与从乙袋中摸出的球不是红球同时发生,由相互独立事件的概率公式可得其概率,对于B,2个球都是红球,即从甲袋中摸出的球是红球与从乙袋中摸出的球是红球同时发生,由相互独立事件的概率公式可得其概率,对于C、至少有1个红球与两球都不是红球为对立事件,由对立事件的概率性质可得其概率,对于D,从甲、乙两袋中摸球有三种情况,即2个球都不是红球,2个球都是红球,2个球中恰有1个红球,由互斥事件的概率性质,可得2个球中恰有1个红球的概率,将求得的概率与![]() 比较,即可得答案.
比较,即可得答案.
解答:解:根据题意,从甲袋中摸出1个红球的概率为![]() ,则摸出的球不是红球的概率为1-
,则摸出的球不是红球的概率为1-![]() =
=![]() ,从乙袋中摸出1个红球的概率为
,从乙袋中摸出1个红球的概率为![]() ,则摸出的球不是红球的概率为1-
,则摸出的球不是红球的概率为1-![]() =
=![]() ,依次分析选项,
,依次分析选项,
对于A、2个球都不是红球,即从甲袋中摸出的球不是红球与从乙袋中摸出的球不是红球同时发生,则其概率为![]() ×
×![]() =
=![]() ,不合题意;
,不合题意;
对于B、2个球都是红球,即从甲袋中摸出的球是红球与从乙袋中摸出的球是红球同时发生,则其概率为![]() ×
×![]() =
=![]() ,不合题意;
,不合题意;
对于C、至少有1个红球与两球都不是红球为对立事件,则其概率为1-![]() =
=![]() ,符合题意;
,符合题意;
对于D、由A可得,2个球都不是红球的概率为![]() ,由B可得2个球都是红球的概率为
,由B可得2个球都是红球的概率为![]() ,则2个球中恰有1个红球的概率为1-
,则2个球中恰有1个红球的概率为1-![]() -
-![]() =
=![]() ,不合题意;
,不合题意;
故选C.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)=x2-(2m+1)x+m.
(1)若方程f(x)=0有两个不等的实根x1,x2,且-1<x1<0<x2<1,求m的取值范围;
(2)若对任意的x∈[1,2],![]() ≤2恒成立,求m的取值范围.
≤2恒成立,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是椭圆
是椭圆![]() :
:![]() (
(![]() )与抛物线
)与抛物线![]() :
:![]() 的一个公共点,且椭圆与抛物线具有一个相同的焦点
的一个公共点,且椭圆与抛物线具有一个相同的焦点![]() .
.
(Ⅰ)求椭圆![]() 及抛物线
及抛物线![]() 的方程;
的方程;
(Ⅱ)设过![]() 且互相垂直的两动直线
且互相垂直的两动直线![]() ,
,![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,
两点,![]() 与抛物线
与抛物线![]() 交于
交于![]() 两点,求四边形
两点,求四边形![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在菱形![]() 中,
中,![]() 且
且![]() ,点
,点![]() 分别是棱
分别是棱![]() 的中点,将四边形
的中点,将四边形![]() 沿着
沿着![]() 转动,使得
转动,使得![]() 与
与![]() 重合,形成如图所示多面体,分别取
重合,形成如图所示多面体,分别取![]() 的中点
的中点![]() .
.

(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)若平面![]() 平面
平面![]() ,求
,求![]() 与平面
与平面![]() 所成的正弦值.
所成的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某超强台风登陆海南省.据统计,本次台风造成全省直接经济损失119.52亿元,适逢暑假,小明调查住在自己小区的50户居民由于台风造成的经济损失,作出如下频率分布直方图:
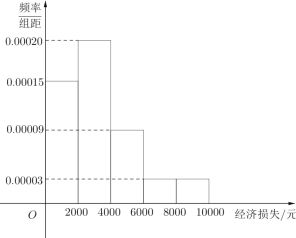
| 经济损失4000元以下 | 经济损失4000元以上 | 合计 |
捐款超过500元 | 30 | ||
捐款低于500元 | 6 | ||
合计 |
台风后区委会号召小区居民为台风重灾区捐款,小明调查的50户居民捐款情况如上表,在表格空白处填写正确数字,并说明是否有![]() 以上的把握认为捐款数额是否多于或少于500元和自身经济损失是否到4000元有关?
以上的把握认为捐款数额是否多于或少于500元和自身经济损失是否到4000元有关?
附:临界值表
| 2.072 | 2.706 | 3.841 | 5.024 | 6635 | 7.879 | 10.828 |
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
参考公式: ![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经销商第一年购买某工厂商品的单价为![]() (单位:元),在下一年购买时,购买单价与其上年度销售额(单位:万元)相联系,销售额越多,得到的优惠力度越大,具体情况如下表:
(单位:元),在下一年购买时,购买单价与其上年度销售额(单位:万元)相联系,销售额越多,得到的优惠力度越大,具体情况如下表:
上一年度 销售额/万元 |
|
|
|
|
|
|
商品单价/元 |
|
|
|
|
|
|
为了研究该商品购买单价的情况,为此调查并整理了![]() 个经销商一年的销售额,得到下面的柱状图.
个经销商一年的销售额,得到下面的柱状图.
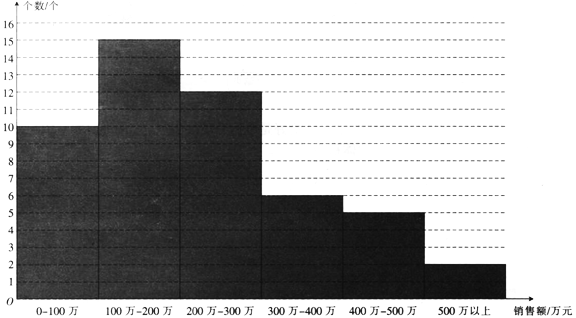
已知某经销商下一年购买该商品的单价为![]() (单位:元),且以经销商在各段销售额的频率作为概率.
(单位:元),且以经销商在各段销售额的频率作为概率.
(1)求![]() 的平均估计值.
的平均估计值.
(2)为了鼓励经销商提高销售额,计划确定一个合理的年度销售额![]() (单位:万元),年销售额超过
(单位:万元),年销售额超过![]() 的可以获得红包奖励,该工厂希望使
的可以获得红包奖励,该工厂希望使![]() 的经销商获得红包,估计
的经销商获得红包,估计![]() 的值,并说明理由.
的值,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com