
ЁОЬтФПЁП1994ФъЕН2016ФъЫљгаЙигкФГЯюбаОПГЩЙћЕФ540ЦЊТлЮФЗжВМШчЯТЭМЫљЪО.
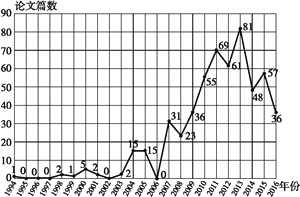
(1)Дгет540ЦЊТлЮФжаЫцЛњГщШЁвЛЦЊРДбаОП,ФЧУДГщЕН2016ФъЗЂБэТлЮФЕФИХТЪЪЧЖрЩй?
(2)ШчЙћУПФъЗЂБэИУСьгђгаЙњМЪгАЯьСІЕФТлЮФГЌЙ§50ЦЊ,ЮвУЧГЦетвЛФъЪЧИУСьгђЕФТлЮФЁАЗсФъЁБ.ШєДг1994ФъЕН2016ФъжаЫцЛњГщШЁСЌајЕФСНФъРДбаОП,ФЧУДСЌајЕФСНФъжажСЩйгавЛФъЪЧЁАЗсФъЁБЕФИХТЪЪЧЖрЩй?
(3)гЩЭМХаЖЯ,ДгФФФъПЊЪМСЌајШ§ФъТлЮФЪ§СПЗНВюзюДѓ?(НсТлВЛвЊЧѓжЄУї)
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉ
ЃЛЃЈ2ЃЉ![]() ЃЛЃЈ3ЃЉМћНтЮі
ЃЛЃЈ3ЃЉМћНтЮі
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉЩшГщЕН2016ФъЗЂБэЕФТлЮФЮЊЪТМў![]() ЃЌРћгУЕШПЩФмЪТМўИХТЪМЦЫуЙЋЪНФмЧѓГіГщЕН2016ФъЗЂБэТлЮФЕФИХТЪЃЛЃЈ2ЃЉЩшжСЩйГщЕНвЛИіЁАЗсФъЁБЮЊЪТМў
ЃЌРћгУЕШПЩФмЪТМўИХТЪМЦЫуЙЋЪНФмЧѓГіГщЕН2016ФъЗЂБэТлЮФЕФИХТЪЃЛЃЈ2ЃЉЩшжСЩйГщЕНвЛИіЁАЗсФъЁБЮЊЪТМў![]() ЃЌРћгУСаОйЗЈФмЧѓГіжСЩйвЛИіЁАЗсФъЁБЕФИХТЪЃЛЃЈ3ЃЉ81ЃЌ48ЃЌ57Ш§ИіЪ§ЗНВюзюДѓЃЌгЩДЫФмЧѓГіНсЙћЃЎ
ЃЌРћгУСаОйЗЈФмЧѓГіжСЩйвЛИіЁАЗсФъЁБЕФИХТЪЃЛЃЈ3ЃЉ81ЃЌ48ЃЌ57Ш§ИіЪ§ЗНВюзюДѓЃЌгЩДЫФмЧѓГіНсЙћЃЎ
ЪдЬтНтЮіЃК(1)ЩшГщЕН2016ФъЗЂБэЕФТлЮФЮЊЪТМўA,вРЬтвтПЩжЊ,P(A)=![]() .
.
(2)ЩшжСЩйГщЕНвЛИіЁАЗсФъЁБЮЊЪТМўB,вРЬтвтПЩжЊ,1994~2016ЕФ23ФъжаЫцЛњГщШЁСЌајСНФъЙВга22жжПЩФм,жСЩйвЛИіЁАЗсФъЁБЕФПЩФмЧщПіга2009~2010,2010~2011,2011~2012,2012~2013,2013~2014,2014~2015,2015~2016ЙВМЦ7жжПЩФм,P(B)=![]() .
.
(3)81,48,57Ш§ИіЪ§ЗНВюзюДѓ,ЫљвдДг2013ФъПЊЪМ,СЌајШ§ФъТлЮФЪ§ЗНВюзюДѓ.


 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖЈвхЗНГЬ ![]() ЕФЪЕЪ§Иљ
ЕФЪЕЪ§Иљ ![]() НазіКЏЪ§
НазіКЏЪ§ ![]() ЕФЁАаТзЄЕуЁБЃЌШєКЏЪ§
ЕФЁАаТзЄЕуЁБЃЌШєКЏЪ§ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЕФЁАаТзЄЕуЁБЗжБ№ЮЊ
ЕФЁАаТзЄЕуЁБЗжБ№ЮЊ ![]() ЃЌдђ
ЃЌдђ ![]() ЕФДѓаЁЙиЯЕЮЊЃЈ ЃЉ
ЕФДѓаЁЙиЯЕЮЊЃЈ ЃЉ
A.![]()
B.![]()
C.![]()
D.![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЪ§Са{an}жаЃЌa1=1ЃЌa2=2ЃЌвдКѓИїЯюгЩan=anЉ1+anЉ2ЃЈnЁн3ЃЉИјГіЃЎ
ЃЈ1ЃЉаДГіДЫЪ§СаЕФЧА5ЯюЃЛ
ЃЈ2ЃЉЭЈЙ§ЙЋЪНbn= ![]() ЙЙдьвЛИіаТЕФЪ§Са{bn}ЃЌаДГіЪ§Са{bn}ЕФЧА4ЯюЃЎ
ЙЙдьвЛИіаТЕФЪ§Са{bn}ЃЌаДГіЪ§Са{bn}ЕФЧА4ЯюЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]()
(I)ЧѓКЏЪ§f(x)ЕФзюаЁе§жмЦкКЭЖдГЦжааФЕФзјБъ
(II)Щш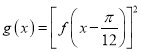 ,ЧѓКЏЪ§g(x)дк
,ЧѓКЏЪ§g(x)дк![]() ЩЯЕФзюДѓжЕ,ВЂШЗЖЈДЫЪБxЕФжЕ
ЩЯЕФзюДѓжЕ,ВЂШЗЖЈДЫЪБxЕФжЕ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЕБ![]() ЪБЃЌЧѓжЄЃК
ЪБЃЌЧѓжЄЃК ![]() КЏЪ§ЪЧХМКЏЪ§ЃЛ
КЏЪ§ЪЧХМКЏЪ§ЃЛ
ЃЈ2ЃЉШєЖдШЮвтЕФ![]() ЃЌЖМга
ЃЌЖМга![]() ЃЌЧѓЪЕЪ§
ЃЌЧѓЪЕЪ§![]() ЕФШЁжЕЗЖЮЇЃЛ
ЕФШЁжЕЗЖЮЇЃЛ
ЃЈ3ЃЉШєКЏЪ§![]() гаЧвНіга
гаЧвНіга![]() ИіСуЕуЃЌЧѓЪЕЪ§
ИіСуЕуЃЌЧѓЪЕЪ§![]() ЕФШЁжЕЗЖЮЇЃЎ
ЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЙ§Ш§ЕуAЃЈЉ3ЃЌ2ЃЉЃЌBЃЈ3ЃЌЉ6ЃЉЃЌCЃЈ0ЃЌ3ЃЉЕФдВЕФЗНГЬЮЊЃЈ ЃЉ
A.x2+y2+4yЉ21=0
B.x2+y2Љ4yЉ21=0
C.x2+y2+4yЉ96=0
D.x2+y2Љ4yЉ96=0
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПСЊКЯЙњНЬПЦЮФзщжЏЙцЖЈЃЌУПФъЕФ4дТ23ШеЪЧЁАЪРНчЖСЪщШеЁБЃЎФГаЃбаОПЩњбЇЯАаЁзщЮЊСЫНтБОаЃбЇЩњЕФдФЖСЧщПіЃЌЫцЛњЕїВщСЫБОаЃ400УћбЇЩњдкетвЛЬьЕФдФЖСЪБМф![]() ЃЈЕЅЮЛЃКЗжжгЃЉЃЌНЋЪБМфЪ§ОнЗжГЩ5зщЃК
ЃЈЕЅЮЛЃКЗжжгЃЉЃЌНЋЪБМфЪ§ОнЗжГЩ5зщЃК![]() ЃЌВЂећРэЕУЕНШчЯТЦЕТЪЗжВМжБЗНЭМЃЎ
ЃЌВЂећРэЕУЕНШчЯТЦЕТЪЗжВМжБЗНЭМЃЎ
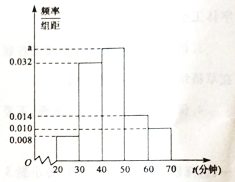
ЃЈ1ЃЉЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ2ЃЉЪдЙРМЦИУбЇаЃЫљгабЇЩњдкетвЛЬьЕФЦНОљдФЖСЪБМфЃЛ
ЃЈ3ЃЉШєгУЗжВуГщбљЕФЗНЗЈДгет400УћбЇЩњжаГщШЁ50ШЫВЮМгНЛСїЛсЃЌдђдкдФЖСЪБМфЮЊ![]() ЕФСНзщжаЗжБ№ГщШЁЖрЩйШЫЃП
ЕФСНзщжаЗжБ№ГщШЁЖрЩйШЫЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЪ§Са{an}Тњзуa1=4ЃЌ2an+1=an+1ЃЎ
ЃЈ1ЃЉЧѓ{an}ЕФЭЈЯюЙЋЪНКЭa5ЃЛ
ЃЈ2ЃЉШєвЊЪЙaЁм ![]() ЃЌЧѓnЕФШЁжЕЗЖЮЇЃЎ
ЃЌЧѓnЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЫФРтзЖ![]() жаЃЌВрУц
жаЃЌВрУц![]() ЮЊЕШБпШ§НЧаЮЧвДЙжБгкЕзУц
ЮЊЕШБпШ§НЧаЮЧвДЙжБгкЕзУц![]() ЃЌ
ЃЌ ![]()
![]() .
.
ЃЈ1ЃЉжЄУїЃК ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШєжБЯп![]() гыЦНУц
гыЦНУц![]() ЫљГЩНЧЮЊ
ЫљГЩНЧЮЊ![]() ЃЌЧѓЖўУцНЧ
ЃЌЧѓЖўУцНЧ![]() ЕФгрЯвжЕ.
ЕФгрЯвжЕ.
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com