
【题目】已知正数数列{xn}满足x1= ![]() ,xn+1=
,xn+1= ![]() ,n∈N* .
,n∈N* .
(1)求x2 , x4 , x6 .
(2)猜想数列{x2n}的单调性,并证明你的结论.
【答案】
(1)解:∵正数数列{xn}满足x1= ![]() ,xn+1=
,xn+1= ![]() ,n∈N*.
,n∈N*.
∴x2= ![]() =
= ![]() .同理可得x4=
.同理可得x4= ![]() ,x6=
,x6= ![]()
(2)解:由x2≥x4≥x6.猜想:数列{x2n}的单调递减.
下面利用数学归纳法证明:①当n=1,2时,命题成立.
②假设当n=k∈N*时命题成立,即x2k>x2k+2,xk>0.
当n=k+1时,x2k+2﹣x2k+4= ![]() ﹣
﹣ ![]() =
= ![]() =
= ![]() >0,即x2(k+1)>x2(k+1)+2,也就是说,当n=k+1时命题也成立.
>0,即x2(k+1)>x2(k+1)+2,也就是说,当n=k+1时命题也成立.
结合①和②知命题成立
【解析】(1)由正数数列{xn}满足x1= ![]() ,xn+1=
,xn+1= ![]() ,n∈N* . 可得x2=
,n∈N* . 可得x2= ![]() =
= ![]() .同理可得x4 , x6 . (2)由x2≥x4≥x6 . 猜想:数列{x2n}的单调递减.利用数学归纳法证明即可得出.
.同理可得x4 , x6 . (2)由x2≥x4≥x6 . 猜想:数列{x2n}的单调递减.利用数学归纳法证明即可得出.
【考点精析】通过灵活运用数列的通项公式,掌握如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式即可以解答此题.


科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() (a>b>0)的左、右焦点分别为F1(﹣3,0)、F2(3,0),直线y=kx与椭圆交于A、B两点.
(a>b>0)的左、右焦点分别为F1(﹣3,0)、F2(3,0),直线y=kx与椭圆交于A、B两点.
(1)若三角形AF1F2的周长为 ![]() ,求椭圆的标准方程;
,求椭圆的标准方程;
(2)若 ![]() ,且以AB为直径的圆过椭圆的右焦点,求直线y=kx斜率k的取值范围.
,且以AB为直径的圆过椭圆的右焦点,求直线y=kx斜率k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某运动员每次投篮命中的概率都是40%.现采用随机模拟的方法估计该运动员三次投篮恰有一次命中的概率:先由计算器产生0到9之间取整数值的随机数,指定1,2,3,4表示命中,5,6,7,8,9,0表示不命中;再以每三个随机数作为一组,代表三次投篮的结果.经随机模拟产生了如下20组随机数:907,966,191,925,271,932,812,458,569,683,431,257,393,027,556,488,730,113,537,989.据此估计,该运动员三次投篮恰有一次命中的概率为( )
A.0.25
B.0.2
C.0.35
D.0.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)在定义域(0,+∞)上为增函数,且满足f(xy)=f(x)+f(y),f(3)=1.
(1)求f(9),f(27)的值;
(2)解不等式f(x)+f(x﹣8)<2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足a1=1,an+1=1﹣ ![]() ,其中n∈N* .
,其中n∈N* .
(1)设bn= ![]() ,求证:数列{bn}是等差数列,并求出{an}的通项公式;
,求证:数列{bn}是等差数列,并求出{an}的通项公式;
(2)设cn= ![]() ,数列{cncn+2}的前n项和为Tn , 求证:Tn<3.
,数列{cncn+2}的前n项和为Tn , 求证:Tn<3.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方体ABCD﹣A′B′C′D′中, ![]() .设点F在线段CC'上,直线EF与平面A'BD所成的角为α,则sinα的取值范围是( )
.设点F在线段CC'上,直线EF与平面A'BD所成的角为α,则sinα的取值范围是( )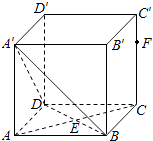
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() ,f′(x)为函数f(x)的导函数.
,f′(x)为函数f(x)的导函数. 
(1)若F(x)=f(x)+b,函数F(x)在x=1处的切线方程为2x+y﹣1=0,求a,b的值;
(2)若f′(x)≤﹣x+ax恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】判断下列各组函数是否为相等函数:
⑴f(x)=f(x)= ![]() ,g(x)=x﹣5;
,g(x)=x﹣5;
⑵f(x)=2x+1(x∈Z),g(x)=2x+1(x∈R);
⑶f(x)=|x+1|,g(x)= ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com