
【题目】某市要对该市六年级学生进行体育素质调查测试,现让学生从“跳绳、短跑![]() 米、长跑
米、长跑![]() 米、仰卧起坐、游泳
米、仰卧起坐、游泳![]() 米、立定跳远”
米、立定跳远”![]() 项中选择
项中选择![]() 项进行测试,其中“短跑、长跑、仰卧起坐”
项进行测试,其中“短跑、长跑、仰卧起坐”![]() 项中至少选择其中
项中至少选择其中![]() 项进行测试.现从该市六年级学生中随机抽取了
项进行测试.现从该市六年级学生中随机抽取了![]() 名学生进行调查,他们选择的项目中包含“短跑、长跑、仰卧起坐”的项目个数及人数统计如下表:(其中
名学生进行调查,他们选择的项目中包含“短跑、长跑、仰卧起坐”的项目个数及人数统计如下表:(其中![]() )
)
选择的项目中包含“短跑、长跑、仰卧起坐”的项目个数 |
|
|
|
人数 |
|
|
|
已知从所调查的![]() 名学生中任选
名学生中任选![]() 名,他们选择“短跑、长跑、仰卧起坐”的项目个数不相等概率为
名,他们选择“短跑、长跑、仰卧起坐”的项目个数不相等概率为![]() ,记
,记![]() 为这
为这![]() 名学生选择“短跑、长跑、仰卧起坐”的项目个数之和.
名学生选择“短跑、长跑、仰卧起坐”的项目个数之和.
(1)求![]() 的值;
的值;
(2)求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lg(ax-bx),(a>1>b>0).
(1)求f(x)的定义域;
(2)若f(x)在(1,+∞)上递增且恒取正值,求a,b满足的关系式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)的定义域为R,且f(2)=2,又函数f(x)的导函数y=f′(x)的图象如图所示,若两个正数a、b满足f(2a+b)<2,则 ![]() 的取值范围是( )
的取值范围是( ) 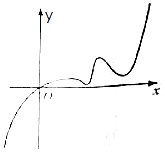
A.( ![]() ,2)
,2)
B.(﹣∞, ![]() )∪(2,+∞)
)∪(2,+∞)
C.(2,+∞)
D.(﹣∞, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从1、2、3、4、5五个数字中任意取出无重复的3个数字.
(I)可以组成多少个三位数?
(II)可以组成多少个比300大的偶数?
(III)从所组成的三位数中任取一个,求该数字是大于300的奇数的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() ,函数
,函数![]() ,
,![]() 是函数
是函数![]() 的导函数,
的导函数, ![]() 是自然对数的底数.
是自然对数的底数.
(1)当![]() 时,求导函数
时,求导函数![]() 的最小值;
的最小值;
(2)若不等式![]() 对任意
对任意![]() 恒成立,求实数
恒成立,求实数![]() 的最大值;
的最大值;
(3)若函数![]() 存在极大值与极小值,求实数
存在极大值与极小值,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某旅游爱好者计划从3个亚洲国家A1,A2,A3和3个欧洲国家B1,B2,B3中选择2个国家去旅游.
(1)若从这6个国家中任选2个,求这2个国家都是亚洲国家的概率;
(2)若从亚洲国家和欧洲国家中各选1个,求这两个国家包括A1,但不包括B1的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面直角坐标系上一动点![]() 到点
到点![]() 的距离是点
的距离是点![]() 到点
到点![]() 的距离的2倍。
的距离的2倍。
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)若点![]() 与点
与点![]() 关于点
关于点![]() 对称,求
对称,求![]() ,
,![]() 两点间距离的最大值。
两点间距离的最大值。
(3)若过点![]() 的直线
的直线![]() 与点
与点![]() 的轨迹
的轨迹![]() 相交于
相交于![]() 、
、![]() 两点,
两点,![]() ,则是否存在直线
,则是否存在直线![]() ,使
,使![]() 取得最大值,若存在,求出此时
取得最大值,若存在,求出此时![]() 的方程,若不存在,请说明理由。
的方程,若不存在,请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com