练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】下列命题正确的是（　　）

    A.“若x＝3，则x2﹣2x﹣3＝0”的否命题是：“若x＝3，则x2﹣2x﹣3≠0”

    B.在△ABC中，“A＞B”是“sinA＞sinB”的充要条件

    C.若p∧q为假命题，则p∨q一定为假命题

    D.“存在x0∈R，使得ex0≤0”的否定是：不存在x0∈R，使得e0”

    【答案】B

    【解析】

    写出命题的否命题判断；中，由正弦定理判断的正误；若“”为假命题，则、至少一个是假命题，判断；利用命题的否定形式判断.

    对于，命题“若，则”的否命题是“若，则”，故不正确．

    对于，中，“” “”；由正弦定理得“” “”；“ ” “”所以正确；

    对于，若“”为假命题，所以、至少一个是假命题，所以错误；

    对于，“存在，使得”的否定是：不存在，使得”，不满足命题的否定形式，所以不正确；

    故选：．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】在一次购物抽奖活动中，已知某10张奖券中有6张有奖，其余4张没有奖，且有奖的6张奖券每张均可获得价值10元的奖品.某顾客从此10张奖券中任意抽取3张.

    （1）求该顾客中奖的概率；

    （2）若约定抽取的3张奖券都有奖时，还要另奖价值6元的奖品，求该顾客获得的奖品总价值（元）的分布列和均值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆，直线不经过椭圆上顶点，与椭圆交于，不同两点.

    （1）当，时，求椭圆的离心率的取值范围；

    （2）若，直线与的斜率之和为，证明：直线过定点.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设数列的前n项和为,对一切,点都在函数的图像上.

    （1）证明：当时,;

    （2）求数列的通项公式;

    （3）设为数列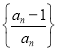的前n项的积,若不等式对一切成立,求实数a的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，已知位于轴左侧的圆与轴相切于点且被轴分成的两段圆弧长之比为，直线与圆相交于，两点，且以为直径的圆恰好经过坐标原点.

    （1）求圆的方程；

    （2）求直线的斜率的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在等腰Rt△ABC中，∠BAC＝90°，腰长为2，D、E分别是边AB、BC的中点，将△BDE沿DE翻折，得到四棱锥B﹣ADEC，且F为棱BC中点，BA.

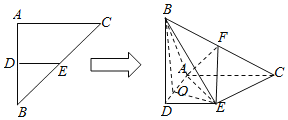
    （1）求证：EF⊥平面BAC；

    （2）在线段AD上是否存在一点Q，使得AF∥平面BEQ？若存在，求二面角Q﹣BE﹣A的余弦值，若不存在，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆C：（）的离心率，左、右焦点分别为，，过右焦点任作一条不垂直于坐标轴的直线l与椭圆C交于A，B两点，的周长为.

    （1）求椭圆C的方程；

    （2）记点B关于x轴的对称点为点，直线交x轴于点D.求的面积的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的右焦点，过的直线交椭圆于、两点，且是线段的中点．

    （1）求椭圆的离心率；

    （2）已知是椭圆的左焦点，求的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥P－ABCD中，PA⊥平面ABCD，AB⊥AD，AD∥BC，AP＝AB＝AD＝1．

    （Ⅰ）若直线PB与CD所成角的大小为，求BC的长；

    （Ⅱ）求二面角B－PD－A的余弦值．

    查看答案和解析>>

    同步练习册答案