Question

13．设函数f（x）=sin（ωx+φ）（ω＞0，-π＜φ＜0）的图象的相邻两对称中心的距离为$\frac{π}{2}$，且过点（$\frac{π}{8}$，-1）．
（1）求函数f（x）的解析式；
（2）五点作图法画出函数f（x）在长度为一个周期的闭区间上的简图；
（3）求方程f（x）-2=m在x∈[$\frac{π}{4}$，$\frac{2π}{3}$]上有解，求m的范围．

Answer 1

分析 （1）根据已知确定函数的频率和初相的值，可得函数f（x）的解析式；
（2）列表求出五个关键点的坐标，进而可得函数的简图；
（3）方程f（x）-2=m在x∈[$\frac{π}{4}$，$\frac{2π}{3}$]上有解，则m+2∈[-$\frac{\sqrt{2}}{2}$，1]，解得答案．

解答 解：（1）∵函数f（x）=sin（ωx+φ）（ω＞0，-π＜ρ＜0）的图象的相邻两对称中心的距离为$\frac{π}{2}$，
∴T=2×$\frac{π}{2}$=π，
又∵ω＞0，
∴ω=$\frac{2π}{π}$=2，
∵函数f（x）=sin（2x+φ）的图象过点（$\frac{π}{8}$，-1）．
∴2×$\frac{π}{8}$+φ=$-\frac{π}{2}$+2kπ，k∈Z，
∴φ=$-\frac{3π}{4}$+2kπ，k∈Z，
又∵-π＜φ＜0，
∴φ=$-\frac{3π}{4}$，
∴f（x）=sin（2x$-\frac{3π}{4}$），
（2）①列表：

x	$\frac{3π}{8}$	$\frac{5π}{8}$	$\frac{7π}{8}$	$\frac{9π}{8}$	$\frac{11π}{8}$
2x$-\frac{3π}{4}$	0	$\frac{π}{2}$	π	$\frac{3π}{2}$	2π
f（x）=sin（2x$-\frac{3π}{4}$）	0	1	0	-1	0

②在坐标系中描出以上五点，
③用光滑的曲线连接这五点，得所要求作的函数图象如下：

（3）由（2）中图象可得：函数f（x）在x∈[$\frac{π}{4}$，$\frac{5π}{8}$]上为增函数，在x∈[$\frac{5π}{8}$，$\frac{2π}{3}$]上减函数，
故当x=$\frac{π}{4}$时，函数取最小值-$\frac{\sqrt{2}}{2}$，当x=$\frac{5π}{8}$时，函数取最大值1，
若方程f（x）-2=m在x∈[$\frac{π}{4}$，$\frac{2π}{3}$]上有解，则m+2∈[-$\frac{\sqrt{2}}{2}$，1]，
则m∈[-2-$\frac{\sqrt{2}}{2}$，-1]

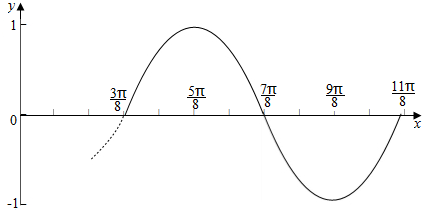
点评 本题考查的知识点是正弦函数的图象和性质，熟练掌握正弦函数的图象和性质，是解答的关键．