
【题目】已知函数f(x)=2x﹣ ![]() . (Ⅰ)若f(x)=2,求x的值;
. (Ⅰ)若f(x)=2,求x的值;
(Ⅱ)若2tf(2t)+mf(t)≥0对于t∈[1,2]恒成立,求实数m的取值范围.
科目:高中数学 来源: 题型:
【题目】如图所示,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD, ![]() ,
, ![]() .
. 
(1)当 ![]() 时,求证:BM∥平面ADEF;
时,求证:BM∥平面ADEF;
(2)若平面BDM与平面ABF所成锐角二面角的余弦值为 ![]() 时,求λ的值.
时,求λ的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某人要利用无人机测量河流的宽度,如图,从无人机A处测得正前方河流的两岸B,C的俯角分别为75°,30°,此时无人机的高是60米,则河流的宽度BC等于( ) 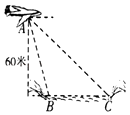
A.![]() 米
米
B.![]() 米
米
C.![]() 米
米
D.![]() 米
米
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有一圆心角为 ![]() ,半径为12cm的扇形铁皮(如图).P,Q是弧AB上的动点且劣弧
,半径为12cm的扇形铁皮(如图).P,Q是弧AB上的动点且劣弧 ![]() 的长为2πcm,过P,Q分别作与OA,OB平行或垂直的线,从扇形上裁剪出多边形OHPRQT,将该多边形面积表示为角α的函数,并求出其最大面积是多少?
的长为2πcm,过P,Q分别作与OA,OB平行或垂直的线,从扇形上裁剪出多边形OHPRQT,将该多边形面积表示为角α的函数,并求出其最大面积是多少? 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,已知射线OA:x﹣y=0(x≥0),OB:2x+y=0(x≥0).过点P(1,0)作直线分别交射线OA,OB于点A,B.
(1)当AB的中点在直线x﹣2y=0上时,求直线AB的方程;
(2)当△AOB的面积取最小值时,求直线AB的方程.
(3)当PAPB取最小值时,求直线AB的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为激励创新,计划逐年加大研发资金投入,若该公司2015年全年投入研发资金超过130万元,在此基础上,每年投入的研发资金比上一年增长12%,则该公司全年投入的研发资金开始超过200万元的年份是年.(参考数据:lg1.12≈0.05,lg1.3≈0.11,lg2≈0.30).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某校高一年级1000名学生中随机抽取100名测量身高,测量后发现被抽取的学生身高全部介于155厘米到195厘米之间,将测量结果分为八组:第一组[155,160),第二组[160,165),…,第八组[190,195),得到频率分布直方图如图所示. (Ⅰ)计算第三组的样本数;并估计该校高一年级1000名学生中身高在170厘米以下的人数;
(Ⅱ)估计被随机抽取的这100名学生身高的中位数、平均数.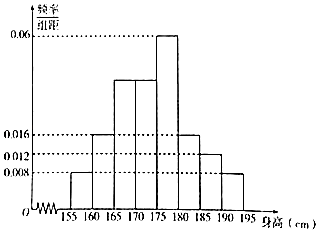
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com