练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如果的三个内角的正弦值分别等于的三个内角的余弦值，则下列正确的是（ ）

    A. 与都是锐角三角形

    B. 与都是钝角三角形

    C. 是锐角三角形且是钝角三角形

    D. 是钝角三角形且是锐角三角形

    【答案】D

    【解析】

    先根据三角形三个内角的余弦值为正数，得出三角形是锐角三角形.先假设三角形分别为锐角三角形或直角三角形，推导出矛盾，由此判断出三角形是钝角三角形.

    因为三角形的三个内角的正弦值都大于零，所以三角形的三个内角的余弦值都大于零，所以三角形是锐角三角形.若三角形是锐角三角形，不妨设,,，即,三个式子相加，得，这与三角形内角和定理矛盾，故三角形不是锐角三角形.若三角形是直角三角形，该直角的正弦值为，对应锐角三角形内角的余弦值为，这个显然不成立，所以三角形不是直角三角形.综上所述，是钝角三角形且是锐角三角形，故选D.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】复利是一种计算利息的方法.即把前一期的利息和本金加在一起算作本金，再计算下一期的利息.某同学有压岁钱1000元，存入银行，年利率为2.25%；若放入微信零钱通或

    者支付宝的余额宝，年利率可达4.01%.如果将这1000元选择合适方式存满5年，可以多获利息( )元.（参考数据：）

    A. 176 B. 100 C. 77 D. 88

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】自点A(-3，3)发出的光线L射到x轴上，被x轴反射，其反射光线所在直线与圆x2+y2-4x-4y+7=0相切，求光线L所在直线的方程。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知在锐角中，角，，所对的边分别为，，，且

    （1）求角大小；

    （2）当时，求的取值范围。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】将一个骰子连续抛掷三次，它落地时向上的点数能组成成等差数列的概率为( )

    A. B. C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】一盒中装有9张各写有一个数字的卡片，其中4张卡片上的数字是1,3张卡片上的数字是2,2张卡片上的数字是3，从盒中任取3张卡片.

    （1）求所取3张卡片上的数字完全相同的概率;

    （2）表示所取3张卡片上的数字的中位数，求的分布列与数学期望.

    （注：若三个数满足，则称为这三个数的中位数）.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

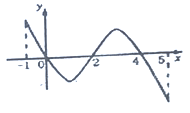
    【题目】已知函数的定义域为，部分对应值如下表，的导函数的图象如图所示，给出关于的下列命题：

    ①函数在处取得极小值;

    ②函数在是减函数，在是增函数；

    ③当时，函数有4个零点；

    ④如果当时，的最大值是2，那么的最小值为0.

    其中所有的正确命题是__________(写出正确命题的序号).

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（题文）已知函数

    （I）当时，求函数的单调区间；

    （II）当时，若对于区间上的任意两个不相等的实数，都有成立，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知等差数列{an}的前n项和为Sn，且2a5－a3＝13，S4＝16．

    （1）求数列{an}的前n项和Sn；

    （2）设Tn＝(－1)iai，若对一切正整数n，不等式 λTn＜[an＋1＋(－1)n＋1an]·2n－1 恒成立，求实数 λ 的取值范围；

    （3）是否存在正整数m，n(n＞m＞2)，使得S2，Sm－S2，Sn－Sm成等比数列？若存在，求出所有的m，n；若不存在，说明理由．

    查看答案和解析>>

    同步练习册答案