Question

给出以下四个结论：
①函数的对称中心是（-1，2）；
②若关于x的方程x-+k=0在x∈（0，1）没有实数根，则k的取值范围是k≥2；
③在△ABC中，“bcosA=acosB”是“△ABC为等边三角形”的必要不充分条件；
④若将函数f（x）=sin（2x-）的图象向右平移φ（φ＞0）个单位后变为偶函数，则φ的最小值是；其中正确的结论是    ．

Answer 1

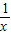【答案】分析：①将函数化为复合函数形式，利用反比例函数的图象性质可得此函数的对称中心；②将问题转化为y=-x在x∈（0，1）上的图象与y=k没有交点问题，利用函数的单调性及数形结合即可得关于x的方程x-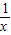+k=0在x∈（0，1）没有实数根的充要条件；③其实若在△ABC中，bcosA=acosB，则sinBcosA-cosAsinB=0，即sin（A-B）=0，即A=B，故三角形定为等腰三角形，不一定为等边三角形；④利用图象变换的理论得平移后函数解析式，再利用函数图象的对称性即可得φ的最小值
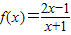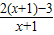解答：解：①函数==2-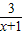，∵f（-1+x）+f（-1-x）=4，∴函数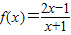的对称中心是（-1，2），①正确；
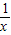②关于x的方程x-+k=0在x∈（0，1）没有实数根，即k=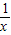-x在x∈（0，1）没有实数根，即y=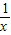-x在x∈（0，1）上的图象与y=k没有交点，
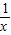∵y=-x在x∈（0，1）上为减函数，∴y＞1-1=0
∴k≤0，∴②错误
③当a=b=1，A=B=30°时，bcosA=acosB，但此三角形不是等边三角形，故，“bcosA=acosB”是“△ABC为等边三角形”的不充分条件；若三角形为等边三角形，则a=b，A=B=60°，
bcosA=acosB，故，“bcosA=acosB”是“△ABC为等边三角形”的必要条件，∴“bcosA=acosB”是“△ABC为等边三角形”的必要不充分条件，③正确
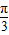④将函数f（x）=sin（2x-）的图象向右平移φ（φ＞0）个单位后的解析式为f（x）=sin（2x-2φ-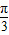），由2φ+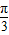=kπ+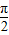，（k∈Z），得φ=kπ+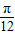，∵φ＞0，∴φ的最小值是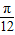；④正确
故答案为①③④
点评：本题考查了复合函数的对称性，函数零点问题与函数图象交点个数的关系，三角变换公式及三角形形状的判断，图象变换与函数图象性质等知识