
【题目】如图所示,在四棱锥![]() 中,
中, ![]() ,
, ![]() 都是等边三角形,平面
都是等边三角形,平面![]() 平面
平面![]() ,且
,且![]() ,
, ![]() .
.
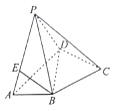
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)![]() 是
是![]() 上一点,当
上一点,当![]() 平面
平面![]() 时,三棱锥
时,三棱锥![]() 的体积.
的体积.
【答案】(Ⅰ)证明见解析;(Ⅱ)6.
【解析】试题分析:
(Ⅰ)要证面面垂直,一般先证线面垂直,也就要证线线垂直,经过计算,得出![]() ,从而有
,从而有![]() ,即
,即![]() ,于是有面面垂直的性质知
,于是有面面垂直的性质知![]() ,从而得证面面垂直;
,从而得证面面垂直;
(Ⅱ)要求三棱锥的体积,关键是找出E点的位置,由于![]() 平面
平面![]() ,可以过BE作与平面PCD平行的平面,交AD于G,则BG//CD,EG//PD,由已知可知
,可以过BE作与平面PCD平行的平面,交AD于G,则BG//CD,EG//PD,由已知可知![]() , 确定了G点,就可确定E点位置,从而求出E到平面PCD的距离,再求得
, 确定了G点,就可确定E点位置,从而求出E到平面PCD的距离,再求得![]() 面积,就有
面积,就有![]() ,从而得所求体积.
,从而得所求体积.
试题解析:
(Ⅰ)因为![]() ,
, ![]() ,
, ![]() ,
,
所以![]() ,所以
,所以![]() ,
, ![]() ,
,
又因为![]() 是等边三角形,所以
是等边三角形,所以![]() ,所以
,所以![]() ,
,
因为平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,
,
因为![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
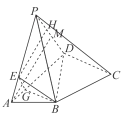
(Ⅱ)过点![]() 作
作![]() 交
交![]() 于
于![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于
于![]() ,
,
因为![]() ,
, ![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
同理可得![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() ,
,
因为![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
因为![]() ,所以
,所以![]() ,在直角三角形
,在直角三角形![]() 中,
中, ![]() ,
, ![]() ,
,
所以![]() ,所以
,所以![]() ,
,
在平面![]() 内过
内过![]() 作
作![]() 于
于![]() ,
,
因为![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,所以
,所以![]() ,
,
因为![]() ,所以
,所以![]() 平面
平面![]() ,所以
,所以![]() 是点
是点![]() 到平面
到平面![]() 的距离,
的距离,
过点![]() 作
作![]() 于
于![]() ,则
,则![]() ,
,
由![]() ,得
,得![]() ,所以
,所以![]() ,
,
因为![]() ,所以
,所以![]() .
.


科目:高中数学 来源: 题型:
【题目】已知点![]() 、
、![]() 的坐标分别是
的坐标分别是![]() ,
,![]() ,直线
,直线![]() ,
,![]() 相交于点
相交于点![]() ,且它们的斜率之积为
,且它们的斜率之积为![]() .
.
(1)求动点![]() 的轨迹方程;
的轨迹方程;
(2)若过点![]() 的直线
的直线![]() 交动点
交动点![]() 的轨迹于
的轨迹于![]() 、
、![]() 两点, 且
两点, 且![]() 为线段
为线段![]() ,
,![]() 的中点,求直线
的中点,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A. “f(0)![]() ”是“函数f(x)是奇函数”的充要条件
”是“函数f(x)是奇函数”的充要条件
B. 若p:![]() ,
,![]() ,则
,则![]() :
:![]() ,
,![]()
C. “若![]() ,则
,则![]() ”的否命题是“若
”的否命题是“若![]() ,则
,则![]() ”
”
D. 若![]() 为假命题,则p,q均为假命题
为假命题,则p,q均为假命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知下列说法:
①命题“x0∈R,x+1>3x0”的否定是“x∈R,x2+1<3x”;
②已知p,q为两个命题,若“p∨q”为假命题,则“¬p∧¬q”为真命题
③“a>2”是“a>5”的充分不必要条件
④“若xy=0,则x=0且y=0”的逆否命题为真命题
其中正确说法的个数为( )
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某蛋糕店制作并销售一款蛋糕,当天每售出![]() 个利润为
个利润为![]() 元,未售出的每个亏损
元,未售出的每个亏损![]() 元.根据以往
元.根据以往![]() 天的统计资料,得到如下需求量表,元旦这天,此蛋糕店制作了
天的统计资料,得到如下需求量表,元旦这天,此蛋糕店制作了![]() 个这种蛋糕.以
个这种蛋糕.以![]() (单位:个,
(单位:个, ![]() )表示这天的市场需求量.
)表示这天的市场需求量. ![]() (单位:元)表示这天售出该蛋糕的利润.
(单位:元)表示这天售出该蛋糕的利润.
需求量/个 |
|
|
|
|
|
天数 | 10 | 20 | 30 | 25 | 15 |
(1)将![]() 表示为
表示为![]() 的函数,根据上表,求利润
的函数,根据上表,求利润![]() 不少于
不少于![]() 元的概率;
元的概率;
![]() 天的平均需求量(同一组数据用该区间的中点值作代表);
天的平均需求量(同一组数据用该区间的中点值作代表);
(3)元旦这天,该店通过微信展示打分的方式随机抽取了![]() 名市民进行问卷调查,调查结果如下表所示,已知在购买意愿强的市民中,女性的占比为
名市民进行问卷调查,调查结果如下表所示,已知在购买意愿强的市民中,女性的占比为![]() .
.
购买意愿强 | 购买意愿弱 | 合计 | |
女性 | 28 | ||
男性 | 22 | ||
合计 | 28 | 22 | 50 |
完善上表,并根据上表,判断是否有![]() 的把握认为市民是否购买这种蛋糕与性别有关?
的把握认为市民是否购买这种蛋糕与性别有关?
附:  .
.
| 0.05 | 0.025 | 0.010 | 0.005 |
| 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=b·ax(其中a,b为常量,且a>0,a≠1)的图象经过点A(1,6),B(3,24).
(1)求f(x);
(2)若不等式(![]() )x+(
)x+(![]() )x-m≥0在x∈(-∞,1]时恒成立,求实数m的取值范围.
)x-m≥0在x∈(-∞,1]时恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知圆
中,已知圆![]() 经过抛物线
经过抛物线![]() 与坐标轴的三个交点.
与坐标轴的三个交点.
(1)求圆![]() 的方程;
的方程;
(2)经过点![]() 的直线
的直线![]() 与圆
与圆![]() 相交于
相交于![]() ,
,![]() 两点,若圆
两点,若圆![]() 在
在![]() ,
,![]() 两点处的切线互相垂直,求直线
两点处的切线互相垂直,求直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com