Question

【题目】已知函数 ．
（1）请在直角坐标系中画出函数f（x）的图象，并写出该函数的单调区间；
（2）若函数g（x）=f（x）﹣m恰有3个不同零点，求实数m的取值范围．

Answer 1

【答案】
（1）解：f（x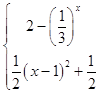）= ，函数f（x）的图象如图所示：

由图象得：函数f（x）的单调递减区间是（0，1），单调增区间是（﹣∞，0），（1，+∞）

（2）解：作出直线y=m，函数g（x）=f（x）﹣m恰有3个不同零点等价于函数y=m与函数f（x）的图象恰有三个不同公共点．

由函数f（x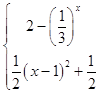）= 的图象易知： ．

故m的取值范围为（ ，1）．

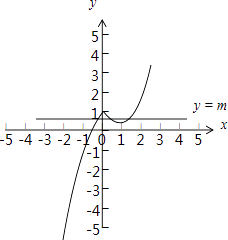
【解析】（1）x≤0的图象部分可由图象变换作出；x＞0的部分为抛物线的一部分．（2）数形结合法：转化为直线y=m与函数f（x）的图象有三个交点．
【考点精析】认真审题，首先需要了解函数图象的作法(图象的作法与平移：①据函数表达式，列表、描点、连光滑曲线；②利用熟知函数的图象的平移、翻转、伸缩变换；③利用反函数的图象与对称性描绘函数图象)，还要掌握函数的单调性(注意：函数的单调性是函数的局部性质；函数的单调性还有单调不增，和单调不减两种)的相关知识才是答题的关键．