�����������⣬�����������εı߳�Ϊ1��������ͼ��ʾ������ϵ����B��1��0����E��-1��1������
=��1��0����
=��-1��1��������
=��+��=����-�̣��̣���
�٣���PΪBC���е㣬
����æˣ��̣������жϳ�����
�ڣ���P��B�غϣ���PΪAD���е㣬��PΪE�㣬�������+��=1�������жϳ�����
�ۣ��������ۣ���P��ABʱ����P��BCʱ����P��CDʱ����P��ADʱ����P��EAʱ����P��DEʱ�����ɵó�����+�̵ķ�Χ�������жϳ�����
�ܣ��ɢ�֪���������+��=k�ĵ�P����ֻ����������k��[1��3]�������жϳ�����
���
�⣺�����⣬�����������εı߳�Ϊ1��������ͼ��ʾ������ϵ��
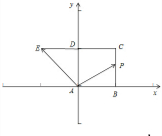
��B��1��0����E��-1��1������
=��1��0����
=��-1��1��������
=��+��=����-�̣��̣���
���ڢ٣��ߵ�PΪBC���е㣬
�����
��=��
��=�����+=��=2���ʢ���ȷ��
���ڢڣ�����=1����=0ʱ��
=��1��0������ʱ��P��B�غϣ������+��=1��
����=
����=
ʱ��
=��0��
������ʱ��PΪAD���е㣬�����+��=1��
����=0����=1����
=����ʱ��PΪE�㣬�����+��=1��
�������+��=1�ĵ�����ֻ���������ʢ���ȷ��
���ڢۣ���P��ABʱ����0�ܦ�-�̡�1����=0���ɵ�0�ܦˡ�1������0�ܦ�+�̡�1��
��P��BCʱ���Ц�-��=1��0�ܦ̡�1������0�ܦ�-1��1����1�ܦˡ�2����1�ܦ�+�̡�3��
��P��CDʱ����0�ܦ�-�̡�1����=1������0�ܦ�-1��1����1�ܦˡ�2����2�ܦ�+�̡�3��
��P��ADʱ���Ц�-��=0��0�ܦ̡�1������0�ܦˡ�1����0�ܦ�+�̡�2��
��P��EAʱ���Ц�=0��0�ܦ̡�1����0�ܦ�+�̡�1��
��P��DEʱ����-1�ܦ�-�̡�0����=1������0�ܦˡ�1����0�ܦ�+�̡�2��
���Ͽɵ�0�ܦ�+�̡�3����C��ȷ��
���ڢܣ��ɢ�֪���������+��=k�ĵ�P����ֻ����������k��[1��3]���ʢܴ���
�ʴ�Ϊ���٢ڢۣ�

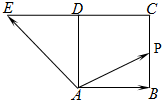 ��ͼ���ı���ABCD�������Σ��ӳ�CD��E��ʹ��DE=CD��������P�ӵ�A�������������εı߰�����·���˶���A��B��C��D��E��A��D������
��ͼ���ı���ABCD�������Σ��ӳ�CD��E��ʹ��DE=CD��������P�ӵ�A�������������εı߰�����·���˶���A��B��C��D��E��A��D������


 ״Ԫ��ȫ��ͻ�Ƶ�����ϵ�д�
״Ԫ��ȫ��ͻ�Ƶ�����ϵ�д� ֱͨ������У�ܲ��¿�ֱͨ��Уϵ�д�
ֱͨ������У�ܲ��¿�ֱͨ��Уϵ�д�
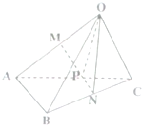 ��ͼ��M��N�ֱ���������OABC����OA��BC���е㣬��P��MN��������
��ͼ��M��N�ֱ���������OABC����OA��BC���е㣬��P��MN��������