
8. 点![]() 在直线
在直线![]() :
:![]() 上,若存在过
上,若存在过![]() 的直线交抛物线
的直线交抛物线![]() 于
于![]() ,
,![]() 两点,且
两点,且![]() ,则称点
,则称点![]() 为“
为“![]() 点”,那么下列结论中正确的是
点”,那么下列结论中正确的是
A.直线![]() 上的所有点都是“
上的所有点都是“![]() 点” B.直线
点” B.直线![]() 上仅有有限个点是“
上仅有有限个点是“![]() 点”
点”
C.直线![]() 上的所有点都不是“
上的所有点都不是“![]() 点” D.直线
点” D.直线![]() 上有无穷多个点(点不是所有的点)是“
上有无穷多个点(点不是所有的点)是“![]() 点”
点”
科目:高中数学 来源: 题型:
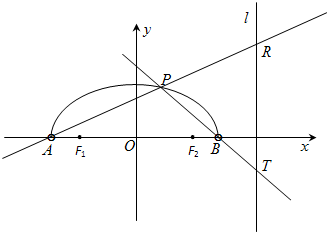 如图,在x轴上方有一段曲线弧Γ,其端点A、B在x轴上(但不属于Γ),对Γ上任一点P及点F1(-1,0),F2(1,0),满足:|PF1|+|PF2|=2
如图,在x轴上方有一段曲线弧Γ,其端点A、B在x轴上(但不属于Γ),对Γ上任一点P及点F1(-1,0),F2(1,0),满足:|PF1|+|PF2|=2| 2 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
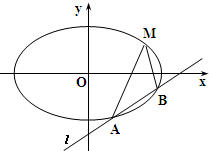 如图,已知焦点在x轴上的椭圆
如图,已知焦点在x轴上的椭圆| x2 |
| 20 |
| y2 |
| b2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 已知椭圆C:
已知椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| PA |
| PF |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 3 |
| 2 |
| PA |
| PB |
| PM |
查看答案和解析>>
科目:高中数学 来源: 题型:
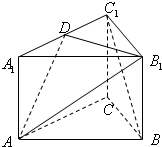 如图,正三棱柱ABC-A1B1C1的底面边长为a,侧棱长为
如图,正三棱柱ABC-A1B1C1的底面边长为a,侧棱长为
| ||
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com