
【题目】如图,在直四棱柱![]() 中,底面四边形
中,底面四边形![]() 是直角梯形,其中
是直角梯形,其中![]() .
.
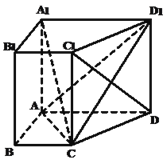
(Ⅰ)求证:直线![]() 平面
平面![]() ;
;
(Ⅱ)试求三棱锥![]() 的体积.
的体积.
【答案】(Ⅰ)证明见解析;(Ⅱ) ![]() .
.
【解析】试题分析:
(Ⅰ)要证线面垂直,一般先证线线垂直,可证得![]() 是正方形,从而有
是正方形,从而有![]() ,再由勾股定理可证
,再由勾股定理可证![]() ,从而得
,从而得![]() 平面
平面![]() ,又得
,又得![]() ,有了两个线线垂直,就可得线面垂直,(注意判定定理的条件要写全);
,有了两个线线垂直,就可得线面垂直,(注意判定定理的条件要写全);
(Ⅱ)由体积性质可得![]() ,即以
,即以![]() 为底面,高为
为底面,高为![]() 的长,易得体积.
的长,易得体积.
试题解析:
(Ⅰ)证明:在梯形ABCD内过C点作![]() 交AD于点
交AD于点![]() ,
,
因为由底面四边形ABCD是直角梯形,
所以![]() ,
,
又![]() ,
,
易知![]() ,且
,且![]() ,
,
所以![]() ,所以
,所以![]()
又根据题意知![]() 面ABCD,从而
面ABCD,从而![]() ,而
,而![]() ,
,
故![]()
因为![]() ,及已知可得
,及已知可得![]() 是正方形,从而
是正方形,从而![]() .
.
因为![]() ,且
,且![]() ,
,
所以![]() 面
面![]()
(Ⅱ)解:
因三棱锥![]() 与三棱锥
与三棱锥![]() 是相同的,故只需求三棱锥
是相同的,故只需求三棱锥![]() 的体积即可,
的体积即可,
而![]() ,且由
,且由![]() 面ABCD可得
面ABCD可得![]() ,又因为
,又因为![]() ,
,
所以有![]() 平面
平面![]() ,即CE为三棱锥
,即CE为三棱锥![]() 的高.
的高.
故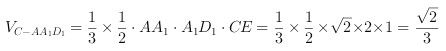


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:高中数学 来源: 题型:
【题目】如图,C、D是以AB为直径的圆上两点,AB=2AD=2 ![]() ,AC=BC,F 是AB上一点,且AF=
,AC=BC,F 是AB上一点,且AF= ![]() AB,将圆沿直径AB折起,使点C在平面ABD的射影E在BD上,已知CE=
AB,将圆沿直径AB折起,使点C在平面ABD的射影E在BD上,已知CE= ![]() .
. 
(1)求证:AD⊥平面BCE;
(2)求证:AD∥平面CEF;
(3)求三棱锥A﹣CFD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设Sn是数列{an}的前n项和. (Ⅰ)若2Sn=3n+3.求{an}的通项公式;
(Ⅱ)若a1=1,an+1﹣an=2n(n∈N*),求Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知各项均为正数的等比数列{an}中,a2=4,a4=16.
(1)求公比q;
(2)若a3 , a5分别为等差数列{bn}的第3项和第5项,求数列{bn}的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从装有![]() 个红球和
个红球和![]() 个黑球的口袋内任取
个黑球的口袋内任取![]() 个球,那么互斥而不对立的两个事件是( )
个球,那么互斥而不对立的两个事件是( )
A. 至少有一个黑球与都是黑球 B. 至少有一个黑球与都是红球
C. 至少有一个黑球与至少有![]() 个红球 D. 恰有
个红球 D. 恰有![]() 个黑球与恰有
个黑球与恰有![]() 个黑球
个黑球
查看答案和解析>>
科目:高中数学 来源: 题型:
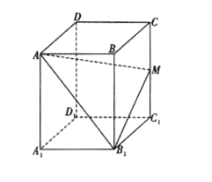
【题目】在边长为2的正方体![]() 中,M是棱CC1的中点.
中,M是棱CC1的中点.
(1)求B到面![]() 的距离;
的距离;
(2)求BC与面![]() 所成角的正切值;
所成角的正切值;
(3)求面![]() 与面ABCD所成的锐二面角的余弦值.
与面ABCD所成的锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某房地产开发公司计划在一楼区内建造一个长方形公园ABCD,公园由长方形的休闲区A1B1C1D1(阴影部分)和环公园人行道组成.已知休闲区A1B1C1D1的面积为4000平方米,人行道的宽分别为4米和10米. 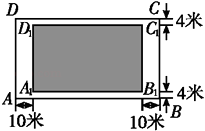
(1)若设休闲区的长A1B1=x米,求公园ABCD所占面积S关于x的函数S(x)的解析式;
(2)要使公园所占面积最小,休闲区A1B1C1D1的长和宽该如何设计?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD的底面是正方形,PD⊥底面ABCD,点E在棱PB上.
(1)求证:平面AEC⊥平面PDB;
(2)当PD=![]() AB,且E为PB的中点时,求AE与平面PDB所成的角的大小.
AB,且E为PB的中点时,求AE与平面PDB所成的角的大小.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() =(2,1),
=(2,1), ![]() =(1,7),
=(1,7), ![]() =(5,1),设R是直线OP上的一点,其中O是坐标原点.
=(5,1),设R是直线OP上的一点,其中O是坐标原点.
(1)求使 ![]() 取得最小值时
取得最小值时 ![]() 的坐标的坐标;
的坐标的坐标;
(2)对于(1)中的点R,求 ![]() 与
与 ![]() 夹角的余弦值.
夹角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com