
一同学在电脑中打出如下若干个圈:○●○○●○○○●○○○○●○○○○○●…若将此若干个圈依此规律继续下去,得到一系列的圈,那么在前120个圈中的●的个数是 ;
14
解析试题分析:把每个实心圆和它前面的连续的空心圆看成一组,那么每组圆的总个数就等于2,3,4,…所以这就是一个等差数列.根据等差数列的求和公式可以算出第120个圆在第15组,且第120个圆不是实心圆,所以前120个圆中有14个实心圆解:将圆分组:第一组:○●,有2个圆;第二组:○○●,有3个圆;第三组:○○○●,有4个圆;…每组圆的总个数构成了一个等差数列,前n组圆的总个数为sn=2+3+4+…+(n+1)=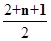 •n,令sn=120,解得n≈14.1,即包含了14整组,即有14个黑圆,故答案为14.
•n,令sn=120,解得n≈14.1,即包含了14整组,即有14个黑圆,故答案为14.
考点:等差数列和归纳猜想
点评:解题的关键是找出图形的变化规律,构造等差数列,然后利用等差数列的求和公式计算.


科目:高中数学 来源: 题型:填空题
如下图①②③④所示,它们都是由小圆圈组成的图案.现按同样的排列规则进行排列,记第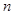 个图形包含的小圆圈个数为
个图形包含的小圆圈个数为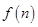 ,则(Ⅰ)
,则(Ⅰ) = ;(Ⅱ)
= ;(Ⅱ) 的个位数字为 .
的个位数字为 .
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
“公差为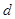 的等差数列
的等差数列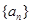 的前
的前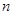 项和为
项和为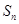 ,则数列
,则数列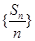 是公差为
是公差为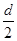 的等差数列”.类比上述性质有:“公比为
的等差数列”.类比上述性质有:“公比为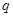 的正项等比数列
的正项等比数列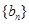 的前
的前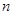 项积为
项积为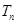 ,则数列____________”.
,则数列____________”.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
半径为r的圆的面积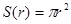 ,周长
,周长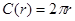 ,若将
,若将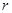 看作(0,+∞)上的变量,则
看作(0,+∞)上的变量,则 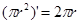 ① , ①式可用语言叙述为:圆的面积函数的导数等于圆的周长函数。
① , ①式可用语言叙述为:圆的面积函数的导数等于圆的周长函数。
对于半径为R的球,若将R看作(0,+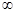 )上的变量,请你写出类似于①的式子:_______________________________________②
)上的变量,请你写出类似于①的式子:_______________________________________②
②式可用语言叙述为___________________。
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
记等差数列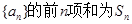 ,利用倒序相加法的求和办法,可将
,利用倒序相加法的求和办法,可将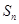 表示成首项
表示成首项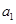 ,末项
,末项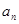 与项数的一个关系式,即
与项数的一个关系式,即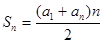 ;类似地,记等比数列
;类似地,记等比数列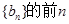 项积为
项积为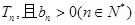 ,类比等差数列的求和方法,可将
,类比等差数列的求和方法,可将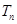 表示为首项
表示为首项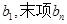 与项数的一个关系式,即公式
与项数的一个关系式,即公式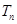 = 。
= 。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com