
���� ���������������Բ���̣�����֪���a����������������b������Բ���̿���
����д��ֱ��l2�ķ��̣�����ֱ�߷��̺���Բ���̣����ø���ϵ���Ĺ�ϵ�õ�M��N���������ĺ�������������������������ʾ���$\overrightarrow{RM}•\overrightarrow{RN}$��Ϊ��ֵ��
��� �⣺��������Բ�ķ���Ϊ$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0����
����Բ�ϵĶ���P����$|{P{F_1}}|+|{P{F_2}}|=4\sqrt{3}$��
��2a=4$\sqrt{3}$��a=2$\sqrt{3}$��
��c=2$\sqrt{2}$����a2=12��b2=a2-c2=4��
����ԲC�ı�����Ϊ$\frac{{x}^{2}}{12}$+$\frac{{y}^{2}}{4}$=1��
������l2��y=kx+1������������$\left\{\begin{array}{l}{y=kx+1}\\{{x}^{2}+3{y}^{2}-12=0}\end{array}\right.$��
��ȥy�ã�1+3k2��x2+6kx-9=0��
�֡ߵ㣨0��1������ԲC�ڣ������0�������
��M ��x1��kx1+1����N��x2��x2+1����
��x1+x2=-$\frac{6k}{1+3{k}^{2}}$��x1x2=-$\frac{9}{1+3{k}^{2}}$��
��֪R��0��-2����$\overrightarrow{RM}$=��x1��kx1+3����$\overrightarrow{RN}$=��x2��kx2+3����
��$\overrightarrow{RM}$•$\overrightarrow{RN}$=x1x2+��kx1+3����kx2+3��=��1+k2��x1x2+3k��x1+x2��+9
=��1+k2��•��-$\frac{9}{1+3{k}^{2}}$��+3k•��-$\frac{6k}{1+3{k}^{2}}$��+9=0����k�أ�
������kȡ��ֵʱ��$\overrightarrow{RM}•\overrightarrow{RN}$��Ϊ��ֵ0��
���� ���⿼����Բ�ļ����ʣ�������ֱ�ߺ�Բ����Ĺ�ϵ��ע���������������飬����Τ�ﶨ��������ƽ�������������������ʾ�������������������������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ��� | [65��75�� | [75��85�� | [85��95�� | [95��105�� | [105��115�� | [115��150�� |
| Ƶ�� | 3 | 4 | 13 | 15 | 10 | 5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ����ֱ��a�ཻ������ֱ��ȷ��һ��ƽ�� | |
| B�� | ����ֱ��ȷ��һ��ƽ�� | |
| C�� | ��һ��ֱ�ߵ�ƽ����������� | |
| D�� | �����ཻƽ��Ľ�����һ���߶� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a+b=22 | B�� | a+b=21 | C�� | ab=20 | D�� | ab=21 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����

| A�� | i��10 | B�� | i��11 | C�� | i��=10 | D�� | i��=11 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
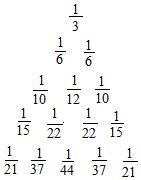 ��ͼ��ʾ�������У���A��m��n����ʾ��m�еĵ�n�����������ι���A��8��2��Ϊ��������
��ͼ��ʾ�������У���A��m��n����ʾ��m�еĵ�n�����������ι���A��8��2��Ϊ��������| A�� | $\frac{1}{45}$ | B�� | $\frac{1}{86}$ | C�� | $\frac{1}{122}$ | D�� | $\frac{1}{167}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{2}$ | B�� | 1 | C�� | $\frac{3}{2}$ | D�� | 4 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com