Question

(1)已知两个等比数列{an},{bn},满足a1=a(a>0),b1-a1=1,b2-a2=2,b3-a3=3,若数列{an}唯一,求a的值;

(2)是否存在两个等比数列{an},{bn},使得b1-a1,b2-a2,b3-a3,b4-a4成公差不为0的等差数列?若存在,求{an},{bn}的通项公式;若不存在,说明理由.

 

Answer 1

【答案】

(1) a= (2) 不存在，理由见解析

【解析】

解:(1)设等比数列{an}的公比为q,

则b1=1+a,b2=2+aq,b3=3+aq2,

由b1,b2,b3成等比数列,得(2+aq)2=(1+a)(3+aq2),

即aq2-4aq+3a-1=0,(*)

由a>0得Δ=4a2+4a>0,故方程(*)有两个不同的实数根,

再由{an}唯一,知方程(*)必有一根为0,将q=0代入方程(*)得a=.

(2)假设存在两个等比数列{an},{bn}使b1-a1,b2-a2,b3-a3,b4-a4成公差不为0的等差数列,设等比数列{an}的公比为q1,等比数列{bn}的公比为q2,

则b2-a2=b1q2-a1q1,

b3-a3=b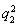1-a1,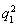

b4-a4=b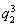1-a1,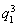

∵b1-a1,b2-a2,b3-a3,b4-a4成等差数列,得

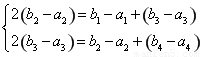
即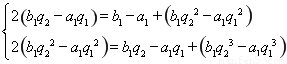

即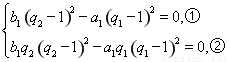

①×q2-②得a1(q1-q2)(q1-1) 2=0,

由a1≠0得q1=q2或q1=1.

(ⅰ)当q1=q2时由①②得b1=a1或q1=q2=1,

这时(b2-a2)-(b1-a1)=0与公差不为0矛盾.

(ⅱ)当q1=1时,由①②得b1=0或q2=1,

这时(b2-a2)-(b1-a1)=0与公差不为0矛盾.

综上所述,不存在两个等比数列{an}{bn}使b1-a1,b2-a2,b3-a3,b4-a4成公差不为0的等差数列.