
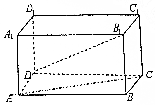
 如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2.
如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2.分析 (Ⅰ)以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,利用向量法能求出异面直线AC与B1D所成角的余弦值.
(Ⅱ)设M到平面ABCD的距离d,则$\frac{{V}_{M-ADC}}{{V}_{ABCD-{A}_{1}{B}_{1}{C}_{1}{D}_{1}}}$=$\frac{\frac{1}{3}{S}_{△ADC}•d}{{S}_{四边形ABCD}•A{A}_{1}}$=$\frac{\frac{1}{6}d}{A{A}_{1}}$=$\frac{1}{18}$,由此能求出结果.
解答 解:(Ⅰ)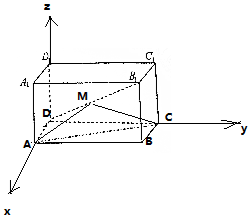 以D为原点,DA为x轴,DC为y轴,DD1为z轴,
以D为原点,DA为x轴,DC为y轴,DD1为z轴,
建立空间直角坐标系,
A(1,0,0),C(0,2,0),B1(1,2,1),
D(0,0,0),
$\overrightarrow{AC}$=(-1,2,0),$\overrightarrow{{B}_{1}D}$=(-1,-2,-1),
设异面直线AC与B1D所成角为θ,
则cosθ=$\frac{|\overrightarrow{AC}•\overrightarrow{{B}_{1}D}|}{|\overrightarrow{AC}|•|\overrightarrow{{B}_{1}D}|}$=$\frac{|-3|}{\sqrt{5}•\sqrt{6}}$=$\frac{\sqrt{30}}{10}$.
∴异面直线AC与B1D所成角的余弦值为$\frac{\sqrt{30}}{10}$.
(Ⅱ)${V}_{ABCD-{A}_{1}{B}_{1}{C}_{1}{D}_{1}}$=S四边形ABCD•AA1,
${S}_{△ADC}=\frac{1}{2}$S四边形ABCD,
设M到平面ABCD的距离d,
∵M是线段B1D上一点,在长方体ABCD-A1B1C1D1内随机选取一点,
该点取自于三棱锥M-ACD内的概率为$\frac{1}{18}$,
∴$\frac{{V}_{M-ADC}}{{V}_{ABCD-{A}_{1}{B}_{1}{C}_{1}{D}_{1}}}$=$\frac{\frac{1}{3}{S}_{△ADC}•d}{{S}_{四边形ABCD}•A{A}_{1}}$=$\frac{\frac{1}{6}d}{A{A}_{1}}$=$\frac{1}{18}$,
解得d=$\frac{A{A}_{1}}{3}$=$\frac{1}{3}$.
设M(a,b,c),$\overrightarrow{DM}$=$λ\overrightarrow{D{B}_{1}}$,则(a,b,c)=(λ,2λ,λ),
∴a=λ,b=2λ,c=λ,
∵d=$\frac{1}{3}$,∴c=λ=$\frac{1}{3}$,∴M($\frac{1}{3},\frac{2}{3},\frac{1}{3}$).
点评 本题考查异面直线所成角的余弦值的求法,考查点的位置的确定,是中档题,解题时要认真审题,注意向量法的合理运用.


科目:高中数学 来源: 题型:填空题
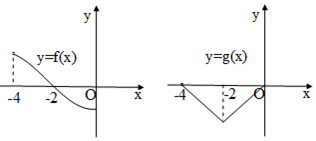 已知偶函数f(x)和奇函数g(x)的定义域都是(-4,4),且在(-4,0]上的图象如图所示,则关于x的不等式f(x)•g(x)<0的解集是(-4,-2)∪(0,2).
已知偶函数f(x)和奇函数g(x)的定义域都是(-4,4),且在(-4,0]上的图象如图所示,则关于x的不等式f(x)•g(x)<0的解集是(-4,-2)∪(0,2).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
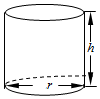 某工厂打算建造如图所示的圆柱形容器(不计厚度,长度单位:米),按照设计要求,该容器的底面半径为r,高为h,体积为16π立方米,且h≥2r.已知圆柱的侧面部分每平方米建造费用为3千元,圆柱的上、下底面部分每平方米建造费用为a千元,假设该容器的建造费用仅与其表面积有关,该容器的建造总费用为y千元.
某工厂打算建造如图所示的圆柱形容器(不计厚度,长度单位:米),按照设计要求,该容器的底面半径为r,高为h,体积为16π立方米,且h≥2r.已知圆柱的侧面部分每平方米建造费用为3千元,圆柱的上、下底面部分每平方米建造费用为a千元,假设该容器的建造费用仅与其表面积有关,该容器的建造总费用为y千元.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=x2-2x+1 | B. | f(x)=x2-1 | C. | f(x)=2x | D. | f(x)=2x+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com