
| t | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| y | 10 | 13 | 9.9 | 7 | 10 | 13 | 10.1 | 7 | 10 |
 =10,
=10,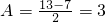
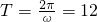 ,
,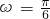 ,
,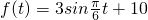 (0≤t≤24)
(0≤t≤24)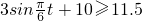
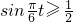 ,
,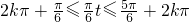
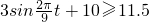 ;再解关于t的三角不等式即可求出船舶在一天中的哪几段时间可以安全的进出该港.
;再解关于t的三角不等式即可求出船舶在一天中的哪几段时间可以安全的进出该港.

科目:高中数学 来源: 题型:
| t | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| y | 10 | 13 | 9.9 | 7 | 10 | 13 | 10.1 | 7 | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| t | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| y | 10.0 | 13.0 | 10.01 | 7.0 | 10.0 | 13.0 | 10.01 | 7.0 | 10.0 |
| A、17 | B、16 | C、5 | D、4 |
查看答案和解析>>
科目:高中数学 来源: 题型:044
某港口的水深y(米)是时间t( ,单位:小时)的函数,下面是水深的数据:
,单位:小时)的函数,下面是水深的数据:
 根据上述数据描出的曲线如下图所示,经拟合,该曲线可近似地看成正弦函数
根据上述数据描出的曲线如下图所示,经拟合,该曲线可近似地看成正弦函数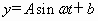 的图象.
的图象.

(1)试根据以上数据,求出 的表达式;
的表达式;
(2)一般情况下,船舶航行时,般底离海底的距离不少于4.5米时是安全的,如果某般的吃水深度(般底与水面的距离)为7米,那么该般在什么时间段能够安全进港?若该般欲当天安全离港,则在港内停留的时间最多不能超过多长时间(忽略进出港所用的时间)?
查看答案和解析>>
科目:高中数学 来源: 题型:
某港口的水深y(米)是时间t(0≤t≤24,单位:小时)的函数,下面是水深数据:
t(时) | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
y(米) | 10.0 | 13.0 | 9.9 | 7.0 | 10.0 | 13.0 | 10.1 | 7.0 | 10.0 |
根据上述数据描出的曲线如下图所示,经拟合,该曲线可近似地看成正弦函数y=Asinωt+b的图象.

(1)试根据以上数据,求出y=Asinωt+b的表达式;
(2)一般情况下,船舶航行时,船底离海底的距离不少于4.5米时是安全的,如果某船的吃水深度(船底与水面的距离)为7米,那么该船在什么时间段能够安全进港?若该船欲当天安全离港,则在港内停留的时间最多不能超过多长时间(忽略进出港所用的时间)?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com