
| A. | (-∞,-1)∪(1,+∞) | B. | (-1,0)∪(0,1) | C. | (1,+∞) | D. | (0,1) |
分析 f(x)=|x|(1+ax)=0,可得x=0或-$\frac{1}{a}$,根据y=f(x+a)是由y=f(x)的图象向左(a>0)或向右(a<0)平移|a|个单位得到,结合关于x的不等式f(x+a)>f(x)对任意x∈R恒成立,可得$\left\{\begin{array}{l}{a>0}\\{-a>-\frac{1}{a}}\end{array}\right.$或$\left\{\begin{array}{l}{a<0}\\{-a<-\frac{1}{a}}\end{array}\right.$,即可得出结论.
解答 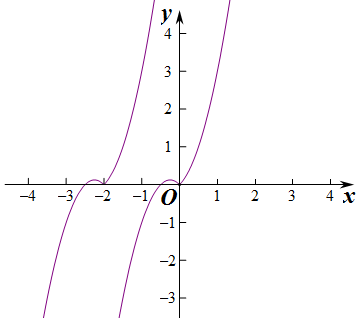 解:f(x)=|x|(1+ax)=0,可得x=0或-$\frac{1}{a}$,
解:f(x)=|x|(1+ax)=0,可得x=0或-$\frac{1}{a}$,
y=f(x+a)是由y=f(x)的图象向左(a>0)或向右(a<0)平移|a|个单位得到,
∵关于x的不等式f(x+a)>f(x)对任意x∈R恒成立,
∴$\left\{\begin{array}{l}{a>0}\\{-a>-\frac{1}{a}}\end{array}\right.$或$\left\{\begin{array}{l}{a<0}\\{-a<-\frac{1}{a}}\end{array}\right.$,
∴a<-1或a>1,
故选A.
点评 本题考查函数的图象变换,考查恒成立问题,考查学生分析解决问题的能力,属于中档题.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:高中数学 来源: 题型:选择题
| A. | {0,1,2} | B. | {0,1,2,3} | C. | {0,1} | D. | {1,2} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (x-1)2+y2=2 | B. | (x-1)2+y2=4 | C. | y2=2x | D. | y2=-2x |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
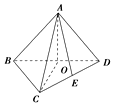 在四面体A-BCD中,AB=BC=CD=AD,∠BAD=∠BCD=90°,二面角A-BD-C为直二面角,E是CD的中点,则∠AED的度数为90°.
在四面体A-BCD中,AB=BC=CD=AD,∠BAD=∠BCD=90°,二面角A-BD-C为直二面角,E是CD的中点,则∠AED的度数为90°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,0)∪(0,1) | B. | (-1,0)∪(1,+∞) | C. | (-∞,-1)∪(1,+∞) | D. | (-∞,-1)∪(0,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com