
【题目】已知函数![]() 为奇函数,曲线
为奇函数,曲线![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 垂直,导函数
垂直,导函数![]() 的最小值为
的最小值为![]() .
.
⑴ 求![]() 的解析式;
的解析式;
⑵ 求![]() 在
在![]() 上的单调增区间、极值、最值.
上的单调增区间、极值、最值.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】如图,在三棱锥V﹣ABC中,平面VAB⊥平面ABC,△VAB为等边三角形,AC⊥BC且AC=BC=![]() ,O,M分别为AB,VA的中点.
,O,M分别为AB,VA的中点.
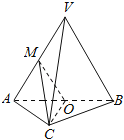
(1)求证:VB∥平面MOC;
(2)求证:平面MOC⊥平面VAB
(3)求三棱锥V﹣ABC的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】十九大以来,某贫困地区扶贫办积极贯彻落实国家精准扶贫的政策要求,带领广大农村地区人民群众脱贫奔小康.经过不懈的奋力拼搏,新农村建设取得巨大进步,农民年收入也逐年增加.为了制定提升农民年收入、实现2020年脱贫的工作计划,该地扶贫办统计了2019年50位农民的年收入并制成如下频率分布直方图:

(1)根据频率分布直方图,估计50位农民的年平均收入![]() 元(单位:千元)(同一组数据用该组数据区间的中点值表示);
元(单位:千元)(同一组数据用该组数据区间的中点值表示);
(2)由频率分布直方图,可以认为该贫困地区农民年收入X服从正态分布![]() ,其中
,其中![]() 近似为年平均收入
近似为年平均收入![]() ,
,![]() 近似为样本方差
近似为样本方差![]() ,经计算得
,经计算得![]() ,利用该正态分布,求:
,利用该正态分布,求:
(i)在扶贫攻坚工作中,若使该地区约有占总农民人数的84.14%的农民的年收入高于扶贫办制定的最低年收入标准,则最低年收入大约为多少千元?
(ii)为了调研“精准扶贫,不落一人”的政策要求落实情况,扶贫办随机走访了1000位农民.若每位农民的年收入互相独立,问:这1000位农民中的年收入不少于12.14千元的人数最有可能是多少?
附参考数据:![]() ,若随机变量X服从正态分布
,若随机变量X服从正态分布![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数![]() 在
在![]() 处取得极大值或极小值,则称
处取得极大值或极小值,则称![]() 为函数
为函数![]() 的极值点.设函数
的极值点.设函数![]() ,
,![]() ,a,b,k
,a,b,k![]() R.
R.
(1)若![]() 为
为![]() 在x=1处的切线.①当
在x=1处的切线.①当![]() 有两个极值点
有两个极值点![]() ,
,![]() ,且满足
,且满足![]() ·
·![]() =1时,求b的值及a的取值范围;②当函数
=1时,求b的值及a的取值范围;②当函数![]() 与
与![]() 的图象只有一个交点,求a的值;
的图象只有一个交点,求a的值;
(2)若对满足“函数![]() 与
与![]() 的图象总有三个交点P,Q,R”的任意突数k,都有PQ=QR成立,求a,b,k满足的条件.
的图象总有三个交点P,Q,R”的任意突数k,都有PQ=QR成立,求a,b,k满足的条件.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂生产某种产品的年固定成本为250万元,每生产![]() 千件,需另投入成本
千件,需另投入成本![]() ,当年产量不足80千件时,
,当年产量不足80千件时,![]() (万元);当年产量不小于80千件时,
(万元);当年产量不小于80千件时,![]() (万元),每件售价为0.05万元,通过市场分析,该厂生产的商品能全部售完.
(万元),每件售价为0.05万元,通过市场分析,该厂生产的商品能全部售完.
(1)写出年利润![]() (万元)关于年产量
(万元)关于年产量![]() (千件)的函数解析式;
(千件)的函数解析式;
(2)年产量为多少千件时,该厂在这一商品的生产中所获利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某校高一1000名学生的物理成绩,随机抽查了部分学生的期中考试成绩,将数据整理后绘制成如图所示的频率分布直方图.
(1)估计该校高一学生物理成绩不低于80分的人数;
(2)若在本次考试中,规定物理成绩在m分以上(包括m分)的为优秀,该校学生物理成绩的优秀率大约为18%,求m的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com