
【题目】椭圆![]() :
:![]() 的左焦点为
的左焦点为![]() 且离心率为
且离心率为![]() ,
,![]() 为椭圆
为椭圆![]() 上任意一点,
上任意一点,![]() 的取值范围为
的取值范围为![]() ,
,![]() .
.
(1)求椭圆![]() 的方程;
的方程;
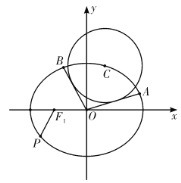
(2)如图,设圆![]() 是圆心在椭圆
是圆心在椭圆![]() 上且半径为
上且半径为![]() 的动圆,过原点
的动圆,过原点![]() 作圆
作圆![]() 的两条切线,分别交椭圆于
的两条切线,分别交椭圆于![]() ,
,![]() 两点.是否存在
两点.是否存在![]() 使得直线
使得直线![]() 与直线
与直线![]() 的斜率之积为定值?若存在,求出
的斜率之积为定值?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
科目:高中数学 来源: 题型:
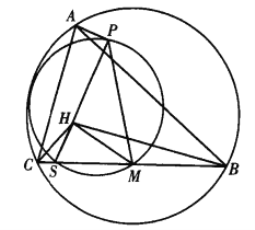
【题目】如图,在![]() 中,AB>AC,H为
中,AB>AC,H为![]() 的垂心,M为边BC的中点,点S在边BC上且满足∠BHM=∠CHS,点A在直线HS上的投影为P.证明:
的垂心,M为边BC的中点,点S在边BC上且满足∠BHM=∠CHS,点A在直线HS上的投影为P.证明:![]() 的外接圆与
的外接圆与![]() 的外接圆相切.
的外接圆相切.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年开始,国家逐步推行全新的高考制度.新高考不再分文理科,采用3+3模式,其中语文、数学、外语三科为必考科目,满分各150分,另外考生还要依据想考取的高校及专业的要求,结合自己的兴趣爱好等因素,在思想政治、历史、地理、物理、化学、生物6门科目中自选3门参加考试(6选3),每科目满分100分.为了应对新高考,某高中从高一年级1000名学生(其中男生550人,女生 450 人)中,采用分层抽样的方法从中抽取![]() 名学生进行调查.
名学生进行调查.
(1)已知抽取的![]() 名学生中含女生45人,求
名学生中含女生45人,求![]() 的值及抽取到的男生人数;
的值及抽取到的男生人数;
(2)学校计划在高一上学期开设选修中的“物理”和“地理”两个科目,为了了解学生对这两个科目的选课情况,对在(1)的条件下抽取到的![]() 名学生进行问卷调查(假定每名学生在这两个科目中必须选择一个科目且只能选择一个科目),下表是根据调查结果得到的
名学生进行问卷调查(假定每名学生在这两个科目中必须选择一个科目且只能选择一个科目),下表是根据调查结果得到的![]() 列联表. 请将列联表补充完整,并判断是否有 99%的把握认为选择科目与性别有关?说明你的理由;
列联表. 请将列联表补充完整,并判断是否有 99%的把握认为选择科目与性别有关?说明你的理由;
(3)在抽取到的45名女生中按(2)中的选课情况进行分层抽样,从中抽出9名女生,再从这9名女生中抽取4人,设这4人中选择“地理”的人数为![]() ,求
,求![]() 的分布列及期望.
的分布列及期望.
选择“物理” | 选择“地理” | 总计 | |
男生 | 10 | ||
女生 | 25 | ||
总计 |
![]() ,其中
,其中![]() .
.
| 0.05 | 0.01 |
| p> | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() 的离心率是
的离心率是![]() ,过点
,过点![]() 做斜率为
做斜率为![]() 的直线
的直线![]() ,椭圆
,椭圆![]() 与直线
与直线![]() 交于
交于![]() 两点,当直线
两点,当直线![]() 垂直于
垂直于![]() 轴时
轴时![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)当![]() 变化时,在
变化时,在![]() 轴上是否存在点
轴上是否存在点![]() ,使得
,使得![]() 是以
是以![]() 为底的等腰三角形,若存在求出
为底的等腰三角形,若存在求出![]() 的取值范围,若不存在说明理由.
的取值范围,若不存在说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 经过点
经过点![]() ,且离心率为
,且离心率为![]() ,过其右焦点F的直线
,过其右焦点F的直线![]() 交椭圆C于M,N两点,交y轴于E点.若
交椭圆C于M,N两点,交y轴于E点.若![]() ,
,![]() .
.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)试判断![]() 是否是定值.若是定值,求出该定值;若不是定值,请说明理由.
是否是定值.若是定值,求出该定值;若不是定值,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com