
【题目】已知直角坐标系![]() 的原点和极坐标系
的原点和极坐标系![]() 的极点重合,
的极点重合,![]() 轴非负半轴与极轴重合, 单位长度相同, 在直角坐标系下, 曲线
轴非负半轴与极轴重合, 单位长度相同, 在直角坐标系下, 曲线![]() 的参数方程为
的参数方程为![]() ,
,![]() 为参数) .
为参数) .
(1) 写出曲线![]() 的极坐标方程;
的极坐标方程;
(2) 直线![]() 的极坐标方程为
的极坐标方程为![]() ,求曲线
,求曲线![]() 与直线
与直线![]() 在平面直角坐标系中的交点坐标 .
在平面直角坐标系中的交点坐标 .
科目:高中数学 来源: 题型:
【题目】新冠肺炎疫情期间,为确保“停课不停学”,各校精心组织了线上教学活动.开学后,某校采用分层抽样的方法从三个年级的学生中抽取一个容量为150的样本进行关于线上教学实施情况的问卷调查.已知该校高一年级共有学生660人,抽取的样本中高二年级有50人,高三年级有45人.下表是根据抽样调查情况得到的高二学生日睡眠时间(单位:h)的频率分布表.
分组 | 频数 | 频率 |
| 5 | 0.10 |
| 8 | 0.16 |
| x | 0.14 |
| 12 | y |
| 10 | 0.20 |
| z | |
合计 | 50 | 1 |
(1)求该校学生总数;
(2)求频率分布表中实数x,y,z的值;
(3)已知日睡眠时间在区间[6,6.5)的5名高二学生中,有2名女生,3名男生,若从中任选2人进行面谈,则选中的2人恰好为一男一女的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】北京地铁八通线西起四惠站,东至土桥站,全长18.964km,共设13座车站.目前八通线执行2014年12月28日制订的计价标准,各站间计程票价(单位:元)如下:
四惠 | 3 | 3 | 3 | 3 | 4 | 4 | 4 | 5 | 5 | 5 | 5 | 5 | |
四惠东 | 3 | 3 | 3 | 4 | 4 | 4 | 5 | 5 | 5 | 5 | 5 | ||
高碑店 | 3 | 3 | 3 | 4 | 4 | 4 | 4 | 5 | 5 | p>5 | |||
传媒大学 | 3 | 3 | 3 | 4 | 4 | 4 | 4 | 5 | 5 | ||||
双桥 | 3 | 3 | 3 | 4 | 4 | 4 | 4 | 4 | |||||
管庄 | 3 | 3 | 3 | 3 | 4 | 4 | 4 | ||||||
八里桥 | 3 | 3 | 3 | 3 | 4 | 4 | |||||||
通州北苑 | 3 | 3 | 3 | 3 | 3 | ||||||||
果园 | 3 | 3 | 3 | 3 | |||||||||
九棵树 | 3 | 3 | 3 | ||||||||||
梨园 | /p> | 3 | 3 | ||||||||||
临河里 | 3 | ||||||||||||
土桥 | |||||||||||||
四惠 | 四惠东 | 高碑店 | 传媒大学 | 双桥 | 管庄 | 八里桥 | 通州北苑 | 果园 | 九棵树 | 梨园 | 临河里 | 土桥 |
(Ⅰ)在13座车站中任选两个不同的车站,求两站间票价不足5元的概率;
(Ⅱ)甲乙二人从四惠站上车乘坐八通线,各自任选另一站下车(二人可同站下车),记甲乙二人乘车购票花费之和为X元,求X的分布列;
(Ⅲ)若甲乙二人只乘坐八通线,甲从四惠站上车,任选另一站下车,记票价为![]() 元;乙从土桥站上车,任选另一站下车,记票价为
元;乙从土桥站上车,任选另一站下车,记票价为![]() 元.试比较
元.试比较![]() 和
和![]() 的方差
的方差![]() 和
和![]() 大小.(结论不需要证明)
大小.(结论不需要证明)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下图是某市![]() 年至
年至![]() 年环境基础设施投资额
年环境基础设施投资额![]() (单位:亿元)的条形图.
(单位:亿元)的条形图.
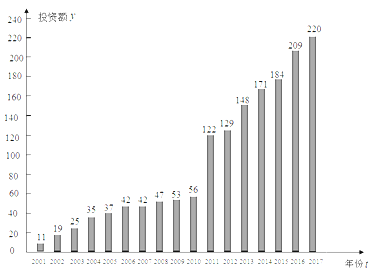
(1)若从![]() 年到
年到![]() 年的五年中,任意选取两年,则这两年的投资额的平均数不少于
年的五年中,任意选取两年,则这两年的投资额的平均数不少于![]() 亿元的概率;
亿元的概率;
(2)为了预测该市![]() 年的环境基础设施投资额,建立了
年的环境基础设施投资额,建立了![]() 与时间变量
与时间变量![]() 的两个线性回归模型.根据
的两个线性回归模型.根据![]() 年至
年至![]() 年的数据(时间变量
年的数据(时间变量![]() 的值依次为
的值依次为![]() )建立模型①:
)建立模型①:![]() ;根据
;根据![]() 年至
年至![]() 年的数据(时间变量
年的数据(时间变量![]() 的值依次为
的值依次为![]() )建立模型②:
)建立模型②:![]() .
.
(i)分别利用这两个模型,求该地区![]() 年的环境基础设施投资额的预测值;
年的环境基础设施投资额的预测值;
(ii)你认为用哪个模型得到的预测值更可靠?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定点M(-3,0),Q、P分别是x轴、y轴上的动点,且使MP⊥PQ,点N在直线PQ上,![]()
(1)求动点N的轨迹C的方程.
(2)过点T(-1,0)作直线l与轨迹C交于两点A、B,问:在x轴上是否存在一点D,使△ABD为等边三角形;若存在,试求出点D的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com