
【题目】设函数f(x)=|x﹣a|,a<0.
(Ⅰ)证明f(x)+f(﹣ ![]() )≥2;
)≥2;
(Ⅱ)若不等式f(x)+f(2x)< ![]() 的解集非空,求a的取值范围.
的解集非空,求a的取值范围.
【答案】(Ⅰ)证明:函数f(x)=|x﹣a|,a<0,
则f(x)+f(﹣ ![]() )=|x﹣a|+|﹣
)=|x﹣a|+|﹣ ![]() ﹣a|
﹣a|
=|x﹣a|+| ![]() +a|≥|(x﹣a)+(
+a|≥|(x﹣a)+( ![]() +a)|
+a)|
=|x+ ![]() |=|x|+
|=|x|+ ![]() ≥2
≥2 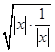 =2.
=2.
(Ⅱ)解:f(x)+f(2x)=|x﹣a|+|2x﹣a|,a<0.
当x≤a时,f(x)=a﹣x+a﹣2x=2a﹣3x,则f(x)≥﹣a;
当a<x< ![]() 时,f(x)=x﹣a+a﹣2x=﹣x,则﹣
时,f(x)=x﹣a+a﹣2x=﹣x,则﹣ ![]() <f(x)<﹣a;
<f(x)<﹣a;
当x ![]() 时,f(x)=x﹣a+2x﹣a=3x﹣2a,则f(x)≥﹣
时,f(x)=x﹣a+2x﹣a=3x﹣2a,则f(x)≥﹣ ![]() .
.
则f(x)的值域为[﹣ ![]() ,+∞),
,+∞),
不等式f(x)+f(2x)< ![]() 的解集非空,即为
的解集非空,即为
![]() >﹣
>﹣ ![]() ,解得,a>﹣1,由于a<0,
,解得,a>﹣1,由于a<0,
则a的取值范围是(﹣1,0)
【解析】(Ⅰ)运用绝对值不等式的性质和基本不等式,即可得证;(Ⅱ)通过对x的范围的分类讨论去掉绝对值符号,转化为一次不等式,求得(f(x)+f(2x))min即可.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中数学 来源: 题型:
【题目】已知△ABC的三个内角A,B,C所对应的边分别为a,b,c,且满足bcosC+ ![]() c=a.
c=a.
(1)求△ABC的内角B的大小;
(2)若△ABC的面积S= ![]() b2 , 试判断△ABC的形状.
b2 , 试判断△ABC的形状.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() ,
,![]() )的一系列对应值如表:
)的一系列对应值如表:

(1)根据表格提供的数据求函数![]() 的一个解析式;
的一个解析式;
(2)根据(1)的结果:
①当![]() 时,方程
时,方程![]() 恰有两个不同的解,求实数
恰有两个不同的解,求实数![]() 的取值范围;
的取值范围;
②若![]() ,
,![]() 是锐角三角形的两个内角,试比较
是锐角三角形的两个内角,试比较![]() 与
与![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】医学上所说的“三高”通常是指血脂增高、血压增高、血糖增高等疾病.为了解“三高”疾病是否与性别有关,医院随机对入院的60人进行了问卷调查,得到了如下的列联表:
(1)请将列联表补充完整;
患三高疾病 | 不患三高疾病 | 合计 | |
男 | 6 | 30 | |
女 | |||
合计 | 36 |
(2)能否在犯错误的概率不超过0.005的前提下认为患“三高”疾病与性别有关? 下列的临界值表供参考:
P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式:K2= ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2 sin(x+![]() )。
)。
(1)若点P(1,-![]() )在角
)在角![]() 的终边上,求:cos
的终边上,求:cos![]() 和f(
和f(![]() -
-![]() )的值;
)的值;
(2)若x![]() [
[![]() ,
, ![]() ],求f(x)的值域。
],求f(x)的值域。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+2x+a,g(x)=lnx﹣2x,如果存在 ![]() ,使得对任意的
,使得对任意的 ![]() ,都有f(x1)≤g(x2)成立,则实数a的取值范围是 .
,都有f(x1)≤g(x2)成立,则实数a的取值范围是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com