
分析 由三角函数公式选择从左往右,或从右往左证明可得.
解答 证明:(1)左边=1+tan2α=1+$\frac{si{n}^{2}α}{co{s}^{2}α}$=$\frac{co{s}^{2}α+si{n}^{2}α}{co{s}^{2}α}$=$\frac{1}{co{s}^{2}α}$=右边;
(2)右边=tan2α-sin2α=$\frac{si{n}^{2}α}{co{s}^{2}α}$-sin2α=$\frac{si{n}^{2}α(1-co{s}^{2}α)}{co{s}^{2}α}$=$\frac{si{n}^{2}αsi{n}^{2}α}{co{s}^{2}α}$=tan2αsin2α=左边;
(3)左边=sin4α+cos4α+2sin2αcos2α-2sin2αcos2α=(sin2α+cos2α)2-2sin2αcos2α=1-2sin2αcos2α=右边;
(4)左边=$\frac{1-2sinxcosx}{co{s}^{2}x-si{n}^{2}x}$=$\frac{si{n}^{2}x+co{s}^{2}x-2sinxcosx}{co{s}^{2}x-si{n}^{2}x}$=$\frac{(cosx-sinx)^{2}}{(cosx+sinx)(cosx-sinx)}$=$\frac{cosx-sinx}{cosx+sinx}$=$\frac{\frac{cosx}{cosx}-\frac{sinx}{cosx}}{\frac{cosx}{cosx}+\frac{sinx}{cosx}}$=$\frac{1-tanx}{1+tanx}$=右边.
点评 本题考查三角函数恒等式的证明,熟练应用三角函数公式是解决问题的关键,属中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
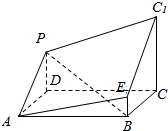 如图所示的多面体是由底面为ABCD的长方体被截面AEC1F所截得到的,其中AB=4,BC=2,CC1=3,BE=1,则点F到平面AEC的距离为( )
如图所示的多面体是由底面为ABCD的长方体被截面AEC1F所截得到的,其中AB=4,BC=2,CC1=3,BE=1,则点F到平面AEC的距离为( )| A. | $\frac{1}{7}$ | B. | $\frac{\sqrt{21}}{7}$ | C. | $\frac{4\sqrt{21}}{7}$ | D. | $\frac{8}{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1-2$\sqrt{2}$,2] | B. | (-∞,-1-2$\sqrt{2}$]∪[2,+∞) | C. | [-1,2] | D. | (-∞,-1]∪[2,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com