
 .
. 在区间
在区间 上的最小值;
上的最小值; ,其中
,其中 ,判断方程
,判断方程 在区间
在区间 上的解的个数(其中
上的解的个数(其中 为无理数,约等于
为无理数,约等于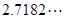 且有
且有 ).
). 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案科目:高中数学 来源:不详 题型:解答题
 .
. 为常数且
为常数且
 时,求
时,求 ;
; 满足
满足 ,但
,但 ,则称
,则称 为
为 的二阶周期点.证明函数
的二阶周期点.证明函数 有且仅有两个二阶周期点,并求二阶周期点
有且仅有两个二阶周期点,并求二阶周期点 ;
; ,设
,设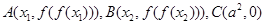 ,记
,记 的面积为
的面积为 ,求
,求 在区间
在区间 上的最大值和最小值。
上的最大值和最小值。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 残骸,我国“雪龙号”科考船于2014年3月26日从港口
残骸,我国“雪龙号”科考船于2014年3月26日从港口 出发,沿北偏东
出发,沿北偏东 角的射线
角的射线 方向航行,而在港口北偏东
方向航行,而在港口北偏东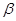 角的方向上有一个给科考船补给物资的小岛
角的方向上有一个给科考船补给物资的小岛 ,
, 海里,且
海里,且
 .现指挥部需要紧急征调位于港口
.现指挥部需要紧急征调位于港口 正东
正东 海里的
海里的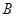 处的补给船,速往小岛
处的补给船,速往小岛 装上补给物资供给科考船.该船沿
装上补给物资供给科考船.该船沿 方向全速追赶科考船,并在
方向全速追赶科考船,并在 处相遇.经测算当两船运行的航线与海岸线
处相遇.经测算当两船运行的航线与海岸线 围成的三角形
围成的三角形 的面积
的面积 最小时,这种补给方案最优.
最小时,这种补给方案最优.
 关于
关于 的函数关系式
的函数关系式 ;
;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,若存在非零常数
,若存在非零常数 ,使函数
,使函数 对于定义域内的任意实数
对于定义域内的任意实数 ,都有
,都有 ,则称函数
,则称函数 是广义周期函数,其中称
是广义周期函数,其中称 为函数
为函数 的广义周期,
的广义周期, 称为周距.
称为周距. 是以2为广义周期的广义周期函数,并求出它的相应周距
是以2为广义周期的广义周期函数,并求出它的相应周距 的值;
的值; ,使
,使 (
( 为常数,
为常数, )为广义周期函数,并求出它的一个广义周期
)为广义周期函数,并求出它的一个广义周期 和周距
和周距 ;
; 是周期
是周期 的周期函数,当函数
的周期函数,当函数 在
在 上的值域为
上的值域为 时,求
时,求 在
在 上的最大值和最小值.
上的最大值和最小值.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 .
. 对所有x∈[﹣1,1],a∈[﹣1,1]恒成立,求实数m的取值范围.
对所有x∈[﹣1,1],a∈[﹣1,1]恒成立,求实数m的取值范围.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
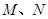 满足条件:①
满足条件:①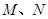 都在函数
都在函数 的图象上;②
的图象上;②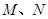 关于原点对称.则称点对
关于原点对称.则称点对 为函数
为函数 的一对“友好点对”.(注:点对
的一对“友好点对”.(注:点对 与
与 为同一“友好点对”).已知函数
为同一“友好点对”).已知函数 ,此函数的友好点对有( )
,此函数的友好点对有( )| A.0对 | B.1对 | C.2对 | D.3对 |

查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 满足
满足 ,当x∈[0,1]时,
,当x∈[0,1]时, ,若在区间(-1,1]上,
,若在区间(-1,1]上, 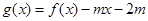 有两个零点,则实数m的取值范围是
有两个零点,则实数m的取值范围是A.0<m≤ | B.0<m< | C. <m≤l <m≤l | D. <m<1 <m<1 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
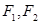 ,我们将图形
,我们将图形 上的任意一点与图形
上的任意一点与图形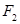 上的任意一点间的距离中的最小值,叫做图形
上的任意一点间的距离中的最小值,叫做图形 与图形
与图形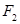 的距离.若两个函数图像的距离小于1,陈这两个函数互为“可及函数”.给出下列几对函数,其中互为“可及函数”的是_________.(写出所有正确命题的编号).
的距离.若两个函数图像的距离小于1,陈这两个函数互为“可及函数”.给出下列几对函数,其中互为“可及函数”的是_________.(写出所有正确命题的编号). ;
; ,
, ;
; ,
, ;
;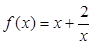 ,
, ;
; ,
,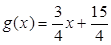 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com