
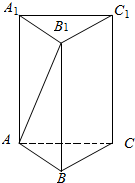
 如图,在正三棱柱ABC-A1B1C1中,若BB1=$\sqrt{2}$,AB=2$\sqrt{2}$,求点C到直线AB1的距离.
如图,在正三棱柱ABC-A1B1C1中,若BB1=$\sqrt{2}$,AB=2$\sqrt{2}$,求点C到直线AB1的距离. 分析 利用几何体求出三角形CAB1的三个边长,然后求解C到直线AB1的距离.
解答  解:在正三棱柱ABC-A1B1C1中,若BB1=$\sqrt{2}$,AB=2$\sqrt{2}$,连结B1C,
解:在正三棱柱ABC-A1B1C1中,若BB1=$\sqrt{2}$,AB=2$\sqrt{2}$,连结B1C,
可得AB1=$\sqrt{{(2\sqrt{2})}^{2}+{(\sqrt{2})}^{2}}$=$\sqrt{10}$,
B1C$\sqrt{{(2\sqrt{2})}^{2}+{(\sqrt{2})}^{2}}$=$\sqrt{10}$
AC=2$\sqrt{2}$.作B1F⊥AC于F,
B1F=$\sqrt{(\sqrt{10})^{2}-(\sqrt{2})^{2}}$=$2\sqrt{2}$,
在三角形ACB1中,CE⊥AB1,CE就是点C到直线AB1的距离:$\frac{AC•{B}_{1}F}{{AB}_{1}}$=$\frac{2\sqrt{2}×2\sqrt{2}}{\sqrt{10}}$=$\frac{4\sqrt{10}}{5}$.
点评 本题考查空间点线面距离的计算,考查计算能力空间想象能力.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:选择题
| A. | ①③ | B. | ①④ | C. | ②③ | D. | ②④ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,点O为作简谐振动的物体的平衡位置,取向右方向为正方向,若振幅为3cm,周期为4s,且物体向右运动到距平衡位置最远处时开始计时.则该物体10s时刻的路程为-3cm.
如图,点O为作简谐振动的物体的平衡位置,取向右方向为正方向,若振幅为3cm,周期为4s,且物体向右运动到距平衡位置最远处时开始计时.则该物体10s时刻的路程为-3cm.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | sin15°cos15° | B. | ${cos^2}\frac{π}{12}-{sin^2}\frac{π}{12}$ | ||
| C. | $\frac{{1+tan{{15}^0}}}{{1-tan{{15}^0}}}$ | D. | $\sqrt{\frac{1+cos30°}{2}}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com