
【题目】已知![]() ,函数
,函数![]() .
.
(1)若函数![]() 在
在![]() 上单调递增,求a的取值范围;
上单调递增,求a的取值范围;
(2)用反证法证明:函数![]() 不可能为
不可能为![]() 上的单调函数.
上的单调函数.
【答案】(1)![]() .(2)证明见解析
.(2)证明见解析
【解析】
(1)函数![]() 在
在![]() 上单调递增,说明
上单调递增,说明![]() ,对于
,对于![]() 都成立,得到
都成立,得到![]() ,令
,令![]() ,则
,则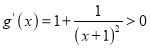 ,转化求解即可;
,转化求解即可;
(2)证明:假设![]() 为
为![]() 上单调函数,则为
上单调函数,则为![]() 上单调递增函数或
上单调递增函数或![]() 上单调递减函数,
上单调递减函数,
①若函数![]() 为
为![]() 上单调递增函数,则
上单调递增函数,则![]() ,对于
,对于![]() 都成立,推出
都成立,推出![]() 不可能为
不可能为![]() 上的单调增函数,②若函数
上的单调增函数,②若函数![]() 为
为![]() 上单调递减函数,则
上单调递减函数,则![]() ,对于
,对于![]() 都成立,推出
都成立,推出![]() 不能为
不能为![]() 上的单调递减函数,说明函数
上的单调递减函数,说明函数![]() 不可能为
不可能为![]() 上的单调函数.
上的单调函数.
(1)函数![]() 在
在![]() 上单调递增,
上单调递增,
所以![]() ,对于
,对于![]() 都成立,
都成立,
即![]() ,对于
,对于![]() 都成立,
都成立,
故有![]() ,
,
令![]() ,则
,则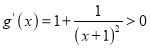 ,
,
故![]() 在
在![]() 上单调递增,
上单调递增,![]() ,
,
∴a的取值范围是![]() ;
;
(2)假设![]() 为R上单调函数,则为R上单调递增函数或R上单调递减函数,
为R上单调函数,则为R上单调递增函数或R上单调递减函数,
①若函数![]() 为R上单调递增函数,则
为R上单调递增函数,则![]() ,对于
,对于![]() 都成立,
都成立,
即![]() 恒成立.
恒成立.
由![]() ,
,![]() 对于
对于![]() 都恒成立,
都恒成立,
由![]() 的开口向上的抛物线,
的开口向上的抛物线,
则![]() ,不可能恒成立,
,不可能恒成立,
所以![]() 不可能为R上的单调增函数;
不可能为R上的单调增函数;
②若函数![]() 为R上单调递减函数,则
为R上单调递减函数,则![]() ,对于
,对于![]() 都成立,
都成立,
即![]() 恒成立,
恒成立,
由![]() ,
,![]() 对于
对于![]() 都恒成立,
都恒成立,
故由![]() ,整理得:
,整理得:![]() ,显然不成立,
,显然不成立,
所以,![]() 不能为R上的单调递减函数,
不能为R上的单调递减函数,
综上,可知函数![]() 不可能为R上的单调函数.
不可能为R上的单调函数.


科目:高中数学 来源: 题型:
【题目】若α是第一象限角,则sinα+cosα的值与1的大小关系是( )
A. sinα+cosα>1B. sinα+cosα=1C. sinα+cosα<1D. 不能确定
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在![]() 的方格表中,每个格被染上红、蓝、黄、绿四种颜色之一,若每个
的方格表中,每个格被染上红、蓝、黄、绿四种颜色之一,若每个![]() 的子方格表包含每种颜色的格均为一,称此染法为“均衡”的.则所有不同的均衡的染法有__________种.
的子方格表包含每种颜色的格均为一,称此染法为“均衡”的.则所有不同的均衡的染法有__________种.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() 在区间
在区间![]() 上的图像如图所示,将该函数图像上各点的横坐标缩短到原来的一半(纵坐标不变),再向右平移
上的图像如图所示,将该函数图像上各点的横坐标缩短到原来的一半(纵坐标不变),再向右平移![]() 个单位长度后,所得到的图像关于直线
个单位长度后,所得到的图像关于直线![]() 对称,则
对称,则![]() 的最小值为( )
的最小值为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某快递公司收取快递费用的标准是:重量不超过![]() 的包裹收费10元;重量超过
的包裹收费10元;重量超过![]() 的包裹,除
的包裹,除![]() 收费10元之外,超过
收费10元之外,超过![]() 的部分,每超出
的部分,每超出![]() (不足
(不足![]() 时按
时按![]() 计算)需再收5元.公司从承揽过的包裹中,随机抽取100件,其重量统计如下:
计算)需再收5元.公司从承揽过的包裹中,随机抽取100件,其重量统计如下:
包裹重量(单位: |
|
|
|
|
|
包裹件数 | 43 | 30 | 15 | 8 | 4 |
公司又随机抽取了60天的揽件数,得到频数分布表如下:
揽件数 |
|
|
|
|
|
天数 | 6 | 6 | 30 | 12 | 6 |
以记录的60天的揽件数的频率作为各揽件数发生的概率
(1)计算该公司3天中恰有2天揽件数在![]() 的概率;
的概率;
(2)估计该公司对每件包裹收取的快递费的平均值;
(3)公司将快递费的三分之一作为前台工作人员的工资和公司利润,剩余的用做其他费用,目前前台有工作人员3人,每人每天揽件不超过150件,每人每天工资100元,公司正在考虑是否将前台工作人员裁减1人,试计算裁员前后公司每日利润的数学期望,并判断裁员是否对提高公司利润有利?
(注:同一组中的揽件数以这组数据所在区间中点值作代表)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() 。
。
Ⅰ.求函数![]() 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;
Ⅱ.当![]() 时,方程
时,方程![]() 恰有两个不同的实数根,求实数
恰有两个不同的实数根,求实数![]() 的取值范围;
的取值范围;
Ⅲ.将函数![]() 的图象向右平移
的图象向右平移![]() 个单位后所得函数
个单位后所得函数![]() 的图象关于原点中心对称,求
的图象关于原点中心对称,求![]() 的最小值。
的最小值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图在四面体![]() 中,
中,![]() 是边长为2的等边三角形,
是边长为2的等边三角形,![]() 为直角三角形,其中
为直角三角形,其中![]() 为直角顶点,
为直角顶点,![]() .
.![]() 分别是线段
分别是线段![]() 上的动点,且四边形
上的动点,且四边形![]() 为平行四边形.
为平行四边形.

(1)求证:![]() 平面
平面![]() ,
,![]() 平面
平面![]() ;
;
(2)试探究当二面角![]() 从0°增加到90°的过程中,线段
从0°增加到90°的过程中,线段![]() 在平面
在平面![]() 上的投影所扫过的平面区域的面积;
上的投影所扫过的平面区域的面积;
(3)设![]()
![]() ,且
,且![]() 为等腰三角形,当
为等腰三角形,当![]() 为何值时,多面体
为何值时,多面体![]() 的体积恰好为
的体积恰好为![]() ?
?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com