
【题目】某次数学知识比赛中共有6个不同的题目,每位同学从中随机抽取3个题目进行作答,已知这6个题目中,甲只能正确作答其中的4个,而乙正确作答每个题目的概率均为![]() ,且甲、乙两位同学对每个题目的作答都是相互独立、互不影响的.
,且甲、乙两位同学对每个题目的作答都是相互独立、互不影响的.
(1)求甲、乙两位同学总共正确作答3个题目的概率;
(2)若甲、乙两位同学答对题目个数分别是![]() ,
,![]() ,由于甲所在班级少一名学生参赛,故甲答对一题得15分,乙答对一题得10分,求甲乙两人得分之和
,由于甲所在班级少一名学生参赛,故甲答对一题得15分,乙答对一题得10分,求甲乙两人得分之和![]() 的期望.
的期望.
科目:高中数学 来源: 题型:
【题目】改革开放以来,伴随着我国经济持续增长,户均家庭教育投入![]() 户均家庭教育投入是指一个家庭对家庭成员教育投入的总和
户均家庭教育投入是指一个家庭对家庭成员教育投入的总和![]() 也在不断提高
也在不断提高![]() 我国某地区2012年至2018年户均家庭教育投入
我国某地区2012年至2018年户均家庭教育投入![]() 单位:千元
单位:千元![]() 的数据如表:
的数据如表:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
户均家庭教育投入y |
|
|
|
|
|
|
|
![]() 求y关于t的线性回归方程;
求y关于t的线性回归方程;
![]() 利用
利用![]() 中的回归方程,分析2012年至2018年该地区户均家庭教育投入的变化情况,并预测2019年该地区户均家庭教育投入是多少.
中的回归方程,分析2012年至2018年该地区户均家庭教育投入的变化情况,并预测2019年该地区户均家庭教育投入是多少.
附:回归直线的斜率和截距的最小二乘法估计公式分别为: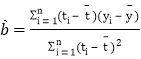 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某企业生产的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量表得如下频数分布表:
质量指标值分组 | [75,85) | [85,95) | [95,105) | [105,115) | [115,125) |
频数 | 6 | 26 | 38 | 22 | 8 |
(I)在答题卡上作出这些数据的频率分布直方图:

(II)估计这种产品质量指标值的平均数及方差(同一组中的数据用该组区间的中点值作代表);
(III)根据以上抽样调查数据,能否认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品的80%”的规定?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】把半椭圆![]() 与圆弧
与圆弧![]() 合成的曲线称作“曲圆”,其中F为半椭圆的右焦点,A是圆弧
合成的曲线称作“曲圆”,其中F为半椭圆的右焦点,A是圆弧![]() 与x轴的交点,过点F的直线交“曲圆”于P,Q两点,则
与x轴的交点,过点F的直线交“曲圆”于P,Q两点,则![]() 的周长取值范围为______
的周长取值范围为______
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点E(﹣4,0)和F(4,0),过点E的直线l与过点F的直线m相交于点M,设直线l的斜率为k1,直线m的斜率为k2,如果k1k2![]() .
.
(1)记点M形成的轨迹为曲线C,求曲线C的轨迹方程.
(2)已知P(2,m)、Q(2,﹣m)(m>0)是曲线C上的两点,A,B是曲线C上位于直线PQ两侧的动点,当A,B运动时,满足∠APQ=∠BPQ,试问直线AB的斜率是否为定值,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com