
【题目】已知二次函数![]() 的对称轴为
的对称轴为![]() ,
,![]() .
.
(1)求函数![]() 的最小值及取得最小值时
的最小值及取得最小值时![]() 的值;
的值;
(2)试确定![]() 的取值范围,使
的取值范围,使![]() 至少有一个实根;
至少有一个实根;
(3)若![]() ,存在实数
,存在实数![]() ,对任意
,对任意![]() ,使
,使![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ,此时
,此时![]() ;(2)
;(2)![]() 的取值范围为
的取值范围为![]() ;(3)实数
;(3)实数![]() 的取值范围为
的取值范围为![]() .
.
【解析】
试题分析:(1)利用基本不等式易得![]() ,此时
,此时![]() .(2)
.(2)![]() 至少有一个实根,即
至少有一个实根,即![]() 与
与![]() 的图象在
的图象在![]() 上至少有一个交点,由题意,可得
上至少有一个交点,由题意,可得![]() ,
,![]() ,则需
,则需![]() 即可;(3)由题意,可得
即可;(3)由题意,可得![]() ,则
,则![]() ,
,
由已知存在实数![]() ,对任意
,对任意![]() ,使
,使![]() 恒成立.即
恒成立.即![]() .令
.令![]() ∴
∴![]() ,转化为存在
,转化为存在![]() ,使
,使![]() 成立.令
成立.令![]() ,
,![]() 的对称轴为
的对称轴为![]() ,分类讨论,即可得到实数
,分类讨论,即可得到实数![]() 的取值范围
的取值范围
试题解析:(1)∵![]() ,∴
,∴![]() ,
,
∴![]() ,当且仅当
,当且仅当![]() ,即
,即![]() 时“=”成立,即
时“=”成立,即![]() ,此时
,此时![]() .
.
(2)![]() 的对称轴为
的对称轴为![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
![]() 至少有一个实根,∴
至少有一个实根,∴![]() 至少有一个实根,
至少有一个实根,
即![]() 与
与![]() 的图象在
的图象在![]() 上至少有一个交点,
上至少有一个交点,
![]() ,∴
,∴![]() ,
,![]() ,
,
∴![]() ,∴
,∴![]() ,∴
,∴![]() 的取值范围为
的取值范围为![]() .
.
(3)![]() ,∴
,∴![]() ,
,
由已知存在实数![]() ,对任意
,对任意![]() ,使
,使![]() 恒成立.
恒成立.
∴![]() .
.
令![]() ,∴
,∴![]() ,即
,即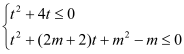 ,
,
转化为存在![]() ,使
,使![]() 成立.
成立.
令![]() ,∴
,∴![]() 的对称轴为
的对称轴为![]() ,
,
∵![]() ,∴
,∴![]() .
.
①当![]() ,即
,即![]() 时,
时,
![]() ,
,
∴![]() ,∴
,∴![]() .
.
②当![]() ,即
,即![]() 时,
时,
![]() ,
,
∴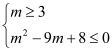 ,∴
,∴![]() ,∴
,∴![]() .
.
综上,实数![]() 的取值范围为
的取值范围为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,某动物园要建造两间完全相同的矩形熊猫居室,其总面积为24平方米,设熊猫居室的一面墙![]() 长为
长为![]() 米(2
米(2![]() ).
).
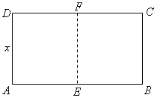
⑴用![]() 表示墙
表示墙![]() 的长;
的长;
⑵假设所建熊猫居室的墙壁造价(在墙壁高度一定的前提下)为每米1000元,请将墙壁的总造价![]() (元)表示为
(元)表示为![]() (米)的函数;
(米)的函数;
⑶当![]() 为何值时,墙壁的总造价最低?
为何值时,墙壁的总造价最低?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为方便市民休闲观光,市政府计划在半径为200米,圆心角为![]() 的扇形广场内(如图所示),沿
的扇形广场内(如图所示),沿![]() 边界修建观光道路,其中
边界修建观光道路,其中![]() 分别在线段
分别在线段![]() 上,且
上,且![]() 两点间距离为定长
两点间距离为定长![]() 米.
米.
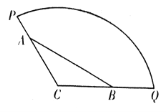
(1)当![]() 时,求观光道
时,求观光道![]() 段的长度;
段的长度;
(2)为提高观光效果,应尽量增加观光道路总长度,试确定图中![]() 两点的位置,使观光道路总长度达到最长?并求出总长度的最大值.
两点的位置,使观光道路总长度达到最长?并求出总长度的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,GH是东西方向的公路北侧的边缘线,某公司准备在GH上的一点B的正北方向的A处建设一仓库,设![]() ,并在公路北侧建造边长为
,并在公路北侧建造边长为![]() 的正方形无顶中转站CDEF(其中EF在GH上),现从仓库A向GH和中转站分别修两条道路AB,AC,已知AB=AC+1,且
的正方形无顶中转站CDEF(其中EF在GH上),现从仓库A向GH和中转站分别修两条道路AB,AC,已知AB=AC+1,且![]() .
.
(1)求![]() 关于
关于![]() 的函数解析式,并求出定义域;
的函数解析式,并求出定义域;
(2)如果中转站四堵围墙造价为10万元/km,两条道路造价为30万元/km,问:![]() 取何值时,该公司建设中转站围墙和两条道路总造价M最低.
取何值时,该公司建设中转站围墙和两条道路总造价M最低.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(必须列式,不能只写答案,答案用数字表示)有4个不同的球,四个不同的盒子,把球全部放入盒内.
(1)求共有多少种放法;
(2)求恰有一个盒子不放球,有多少种放法;
(3)求恰有两个盒内不放球,有多少种放法;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,四边形ABCD是矩形,侧面PAD⊥底面ABCD,若点E,F分别是PC,BD的中点。
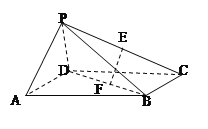
(1)求证:EF∥平面PAD;
(2)求证:平面PAD⊥平面PCD
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com