
如图,五面体中,四边形ABCD是矩形,DA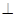 面ABEF,且DA=1,AB//EF,
面ABEF,且DA=1,AB//EF, ,P、Q、M分别为AE、BD、EF的中点.
,P、Q、M分别为AE、BD、EF的中点.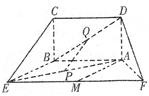
求证:(I)PQ//平面BCE;
(II)求证:AM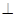 平面ADF;
平面ADF;
(I)见解析(II)见解析.
解析试题分析:(I)连接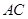 ,根据四边形ABCD是矩形,Q为BD的中点,推出Q为AC的中点,利用
,根据四边形ABCD是矩形,Q为BD的中点,推出Q为AC的中点,利用 从而可得PQ//平面BCE.
从而可得PQ//平面BCE.
(II)由M是EF的中点,得到EM=AB=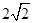 ,
,
推出四边形ABEM是平行四边形.
从而由AM//BE,AM=BE=2,AF=2,MF=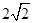 ,得到
,得到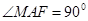 ,
,
推出 .又可得
.又可得 ,即可得出AM
,即可得出AM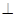 平面ADF.
平面ADF.
试题解析:(I)连接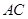 ,因为四边形ABCD是矩形,Q为BD的中点,所以,Q为AC的中点,
,因为四边形ABCD是矩形,Q为BD的中点,所以,Q为AC的中点,
又在 中,
中, 为
为 的中点,所以
的中点,所以 ,
,
因为,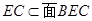 ,
, ,所以,PQ//平面BCE.
,所以,PQ//平面BCE.
(II)因为,M是EF的中点,所以,EM="AB=" 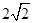 ,
,
又因为EF//AB,所以,四边形ABEM是平行四边形.
所以,AM//BE,AM=BE=2,
又AF=2,MF=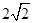 ,所以,
,所以,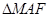 是直角三角形,且
是直角三角形,且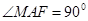 ,
,
所以, .
.
又因为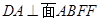 ,
, 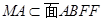 ,
,
所以, ,
,
又 ,所以,AM
,所以,AM 平面ADF.
平面ADF.
考点:平行关系,垂直关系.


 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源: 题型:解答题
如图,正三棱柱ABC-A'B'C'中,D是BC的中点,AA'=AB=2.
(1)求证:A'C//平面AB'D;
(2)求二面角D一AB'一B的余弦值。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图所示,已知三棱锥A-BPC中,AP⊥PC,AC⊥BC,M为AB的中点,D为PB的中点,且△PMB为正三角形.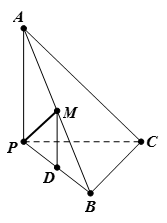
(1)求证:DM∥平面APC; (2)求证:平面ABC⊥平面APC.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,在直三棱柱ABC—A1B1C1中,  ,直线B1C与平面ABC成45°角。
,直线B1C与平面ABC成45°角。
(1)求证:平面A1B1C⊥平面B1BCC1;
(2)求二面角A—B1C—B的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在三棱柱ABC-A1B1C1中,AB=BC=CA=AA1=2,侧棱AA1⊥面ABC,D、E分别是棱A1B1、AA1的中点,点F在棱AB上,且

(I)求证:EF∥平面BDC1;
(II)求二面角E-BC1-D的余弦值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com