
【题目】在三棱台![]() 中,
中,![]() 是等边三角形,二面角
是等边三角形,二面角![]() 的平面角为
的平面角为![]() ,
,![]() .
.
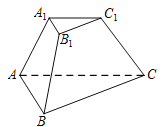
(I)求证:![]() ;
;
(II)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(Ⅰ)见证明;(Ⅱ)![]()
【解析】
(I)先由线面垂直的判定定理证明![]() 平面
平面![]() ,进而可得
,进而可得![]() ;
;
(II)可以在几何体中作出直线![]() 与平面
与平面![]() 所成的角,解三角形即可;也可用向量的方法建立适当的坐标系,求出直线的方向向量以及平面的法向量,根据向量夹角的余弦值确定线面角的正弦值.
所成的角,解三角形即可;也可用向量的方法建立适当的坐标系,求出直线的方向向量以及平面的法向量,根据向量夹角的余弦值确定线面角的正弦值.
(I)证明:设![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,取棱
,取棱![]() 的中点
的中点![]() ,连结
,连结![]() .
.
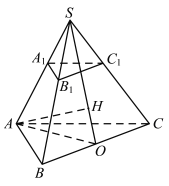
因![]() ,
,![]() ,
,
故![]() .
.
又![]() 是棱
是棱![]() 的中点,
的中点,
故![]() .
.
同理![]()
又![]() 平面
平面![]() ,且
,且![]() ,
,
因此![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,
,
所以![]() ;
;
(II)方法一:
作![]() ,垂足为
,垂足为![]() .
.
因![]() 平面
平面![]() ,
,
故![]() 平面
平面![]() ,
,
从而![]() 为直线
为直线![]() 与平面
与平面![]() 所成的角.
所成的角.
不妨设![]() ,则
,则![]() ,
,![]() ,
,
所以![]() .
.
方法二:如图,以![]() 为原点建立空间直角坐标系
为原点建立空间直角坐标系![]() ,
,
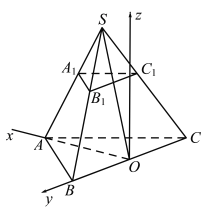
由(I),![]() 为二面角
为二面角![]() 的平面角,则
的平面角,则![]() ,
,
设![]() ,
,![]() ,则点
,则点![]() ,
,![]() ,
,![]() ,
,![]() .
.
设![]() 为平面
为平面![]() ,即平面
,即平面![]() 的一个法向量,
的一个法向量,
由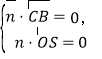 ,得
,得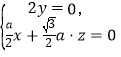 ,
,
令![]() ,则
,则![]() ,即
,即![]() .
.
![]() .
.
设![]() 是直线
是直线![]() 与平面
与平面![]() 所成的角,
所成的角,
则![]() .
.


科目:高中数学 来源: 题型:
【题目】奥运会排球预选赛有![]() 支球队参加,其中每两队比赛一场,每场比赛必决出胜负。如果其中有
支球队参加,其中每两队比赛一场,每场比赛必决出胜负。如果其中有![]() 支球队
支球队![]() 满足:
满足:![]() 胜
胜![]() ,
,![]() 胜
胜![]() ,
,![]() 胜
胜![]() ,
,![]() 胜
胜![]() ,则称这
,则称这![]() 支球队组成一个“
支球队组成一个“![]() 阶连环套”。证明:若全部
阶连环套”。证明:若全部![]() 支球队组成一个
支球队组成一个![]() 阶连环套,则对于每个
阶连环套,则对于每个![]() 及每支球队
及每支球队![]() ,
,![]() 必与另外某些球队组成一个
必与另外某些球队组成一个![]() 阶连环套。
阶连环套。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着手机的发展,“微信”逐渐成为人们支付购物的一种形式.某机构对“使用微信支付”的态度进行调查,随机抽取了50人,他们年龄的频数分布及对“使用微信支付”赞成人数如下表.
年龄(单位:岁) |
|
|
|
|
|
|
频数 | 5 | 10 | 15 | 10 | 5 | 5 |
赞成人数 | 5 | 10 | 12 | 7 | 2 | 1 |
(1)若以“年龄45岁为分界点”,由以上统计数据完成下面![]() 列联表,并判断是否有99%
列联表,并判断是否有99%
年龄不低于45岁的人数 | 年龄低于45岁的人数 | 合计 | |
赞成 | |||
不赞成 | |||
合计 |
(2)若从年龄在![]() 的被调查人中按照赞成与不赞成分层抽样,抽样人数分别3人与2人,现对抽样的5人进行追踪调查,在5人中抽取3人做专访,求3人中不赞成使用微信支付的人数的分布列和期望值.
的被调查人中按照赞成与不赞成分层抽样,抽样人数分别3人与2人,现对抽样的5人进行追踪调查,在5人中抽取3人做专访,求3人中不赞成使用微信支付的人数的分布列和期望值.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
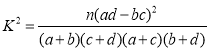 ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知钝角△ABC中,∠B-∠C=90°,∠C=θ,其外接圆⊙O的半径为R.AD是⊙O的一条直径,过点D作⊙O的切线与BC的延长线交于H,过点D作BA的平行线交AC的延长线于E,交过D、O、H的圆于G,联结GH、EH.求△EGH的面积.
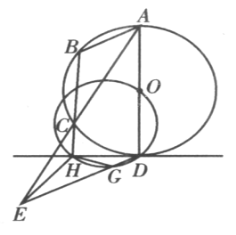
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了研究某学科成绩是否与学生性别有关,采用分层抽样的方法,从高二年级抽取了![]() 名男生和
名男生和![]() 名女生的该学科成绩,得到如图所示男生成绩的频率分布直方图和女生成绩的茎叶图,规定
名女生的该学科成绩,得到如图所示男生成绩的频率分布直方图和女生成绩的茎叶图,规定![]() 分以上为优分(含
分以上为优分(含![]() 分).
分).

(1)(i)请根据图示,将2×2列联表补充完整;
优分 | 非优分 | 总计 | |
男生 | |||
女生 | |||
总计 | 50 |
(ii)据列联表判断,能否在犯错误概率不超过![]() 的前提下认为“学科成绩与性别有关”?
的前提下认为“学科成绩与性别有关”?
(2)将频率视作概率,从高二年级该学科成绩中任意抽取![]() 名学生的成绩,求成绩为优分人数
名学生的成绩,求成绩为优分人数![]() 的分布列与数学期望.
的分布列与数学期望.
参考公式: .
.
参考数据:
| 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知曲线
中,已知曲线![]() 的参数方程为
的参数方程为![]() ,(
,(![]() 为参数),点
为参数),点![]() .以坐标原点
.以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)试判断点![]() 是否在直线
是否在直线![]() 上,并说明理由;
上,并说明理由;
(2)设直线![]() 与曲线
与曲线![]() 交于点
交于点![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列有关命题的说法正确的是___(请填写所有正确的命题序号).
①命题“若![]() ,则
,则![]() ”的否命题为:“若
”的否命题为:“若![]() ,则
,则![]() ”;
”;
②命题“若![]() ,则
,则![]() ”的逆否命题为真命题;
”的逆否命题为真命题;
③条件![]() ,条件
,条件![]() ,则
,则![]() 是
是![]() 的充分不必要条件;
的充分不必要条件;
④已知![]() 时,
时,![]() ,若
,若![]() 是锐角三角形,则
是锐角三角形,则![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋内有大小完全相同的![]() 个黑球和
个黑球和![]() 个白球,从中不放回地每次任取
个白球,从中不放回地每次任取![]() 个小球,直至取到白球后停止取球,则( )
个小球,直至取到白球后停止取球,则( )
A.抽取![]() 次后停止取球的概率为
次后停止取球的概率为![]()
B.停止取球时,取出的白球个数不少于黑球的概率为![]()
C.取球次数![]() 的期望为
的期望为![]()
D.取球次数![]() 的方差为
的方差为![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com