设数列{an}的前n项和为Sn,且方程x2-anx-an=0有一根为Sn-1,n=1,2,3,….
(Ⅰ)求a1,a2;
(Ⅱ){an}的通项公式.
解:(Ⅰ)当n=1时,x
2-a
1x-a
1=0有一根为S
1-1=a
1-1,
于是(a
1-1)
2-a
1(a
1-1)-a
1=0,解得a
1=

.
当n=2时,x
2-a
2x-a
2=0有一根为S
2-1=a
2-

,
于是(a
2-

)
2-a
2(a
2-

)-a
2=0,解得a
2=

.
(Ⅱ)由题设(S
n-1)
2-a
n(S
n-1)-a
n=0,
即S
n2-2S
n+1-a
nS
n=0.
当n≥2时,a
n=S
n-S
n-1,代入上式得
S
n-1S
n-2S
n+1=0 ①
由(Ⅰ)知S
1=a
1=

,S
2=a
1+a
2=

+

=

.
由①可得S
3=

.
由此猜想S
n=

,n=1,2,3,….
下面用数学归纳法证明这个结论.
(i)n=1时已知结论成立.
(ii)假设n=k时结论成立,即S
k=

,
当n=k+1时,由①得S
k+1=
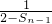
,即S
k+1=
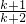
,
故n=k+1时结论也成立.
综上,由(i)、(ii)可知S
n=

对所有正整数n都成立.
于是当n≥2时,a
n=S
n-S
n-1=

-

=

,
又n=1时,a
1=

=

,所以{a
n}的通项公式a
n=

,n=1,2,3,….
分析:(Ⅰ)分别取n=1,n=2,根据方程x
2-a
nx-a
n=0有一根为S
n-1,即可求得a
1,a
2;
(Ⅱ)由题设(S
n-1)
2-a
n(S
n-1)-a
n=0,即S
n2-2S
n+1-a
nS
n=0,当n≥2时,a
n=S
n-S
n-1,代入上式得S
n-1S
n-2S
n+1=0,通过计算猜想S
n=

,n=1,2,3,….再用数学归纳法证明这个结论,进而利用当n≥2时,a
n=S
n-S
n-1=

-

=

,n=1时,a
1=

=

,即可求得{a
n}的通项公式.
点评:本题重点考查数学归纳法,考查数列的通项,先猜后证是关键,注意数学归纳法的证题步骤,属于中档题.

 .
. ,
, )2-a2(a2-
)2-a2(a2- )-a2=0,解得a2=
)-a2=0,解得a2= .
. ,S2=a1+a2=
,S2=a1+a2= +
+ =
= .
. .
. ,n=1,2,3,….
,n=1,2,3,…. ,
,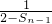 ,即Sk+1=
,即Sk+1=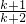 ,
, 对所有正整数n都成立.
对所有正整数n都成立. -
- =
= ,
, =
= ,所以{an}的通项公式an=
,所以{an}的通项公式an= ,n=1,2,3,….
,n=1,2,3,…. ,n=1,2,3,….再用数学归纳法证明这个结论,进而利用当n≥2时,an=Sn-Sn-1=
,n=1,2,3,….再用数学归纳法证明这个结论,进而利用当n≥2时,an=Sn-Sn-1= -
- =
= ,n=1时,a1=
,n=1时,a1= =
= ,即可求得{an}的通项公式.
,即可求得{an}的通项公式.

 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案