Question

【题目】求证:对任何a>0,b>0,c>0,都

Answer 1

【答案】见解析.

【解析】

注意,这是以a,b为边长且夹角为60°的三角形的第三边的边长.同b,c为边长且夹角为60°的三角形的第三边的边长.a,c为边长且夹角为120°的三角形的第三边的边长.于是可将a,b,c三者归结到三角形中,并从中证得不等式. 注意,这是以a,b为边长且夹角为60°的三角形的第三边的边长.同b,c为边长且夹角为60°的三角形的第三边的边长.a,c为边长且夹角为120°的三角形的第三边的边长.于是可将a,b,c三者归结到三角形中,并从中证得不等式.

证明构造平面图形如图所示,其中OA=a,OB=b,OC=c,∠AOB=∠BOC=60°.

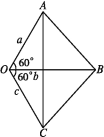
由余弦定理,得

，

，

因为AB+BC≥AC,所以有

，

其中等号成立的充要条件是AB+BC=AC,即A,B,C在同一条直线上,此时S△AOC=S△AOB+S△BOC,

120°60°60°,

即ac=ab+bc.

两边同除以abc,

即等号成立的充要条件