
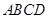 是边长为2的正方形,
是边长为2的正方形,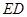 ⊥平面
⊥平面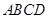 ,
, ,
,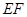 //
// 且
且 .
.
 ⊥平面
⊥平面 ;
; 的体积.
的体积.  ⊥平面
⊥平面 ;(Ⅱ)采用体积分割的思路进行求解.即
;(Ⅱ)采用体积分割的思路进行求解.即 ,然后明确几何体的高进行求解.
,然后明确几何体的高进行求解.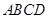 ,AC
,AC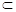 平面
平面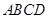 ,∴ ED⊥AC. 2分
,∴ ED⊥AC. 2分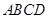 是正方形,∴ BD⊥AC, 4分
是正方形,∴ BD⊥AC, 4分
 DO,∴ 四边形EFOD是平行四边形.
DO,∴ 四边形EFOD是平行四边形.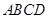 可得ED⊥DO,
可得ED⊥DO, ∥
∥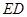 ,
,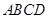 ,∴
,∴  ⊥平面
⊥平面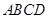 .
. 是边长为2的正方形,∴
是边长为2的正方形,∴ .
. 、
、 到平面BDEF的距离分别是
到平面BDEF的距离分别是 、
、 ,
, ;
; . 10分
. 10分



科目:高中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 为圆心,
为圆心, 为半径画圆弧
为半径画圆弧 ,裁剪的扇形
,裁剪的扇形 围成一个圆锥的侧面,余下的部分裁剪出它的底面.当圆锥的侧面积最大时,圆锥底面的半径
围成一个圆锥的侧面,余下的部分裁剪出它的底面.当圆锥的侧面积最大时,圆锥底面的半径 .
.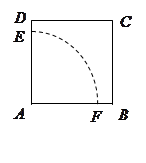
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com