
【题目】为响应国家扩大内需的政策,某厂家拟在2016年举行某一产品的促销活动,经调查测算,该产品的年销量(即该厂的年产量)![]() 万件与年促销费用
万件与年促销费用![]() (
(![]() )万元满足
)万元满足![]() (
(![]() 为常数).如果不搞促销活动,则该产品的年销量只能是1万件.已知2016年生产该产品的固定投入为6万元,每生产1万件该产品需要再投入12万元,厂家将每件产品的销售价格定为每件产品平均生产投入成本的1.5倍(生产投入成本包括生产固定投入和生产再投入两部分).
为常数).如果不搞促销活动,则该产品的年销量只能是1万件.已知2016年生产该产品的固定投入为6万元,每生产1万件该产品需要再投入12万元,厂家将每件产品的销售价格定为每件产品平均生产投入成本的1.5倍(生产投入成本包括生产固定投入和生产再投入两部分).
(1)求常数![]() ,并将该厂家2016年该产品的利润
,并将该厂家2016年该产品的利润![]() 万元表示为年促销费用
万元表示为年促销费用![]() 万元的函数;
万元的函数;
(2)该厂家2016年的年促销费用投入多少万元时,厂家利润最大?
 小题狂做系列答案
小题狂做系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),曲线
为参数),曲线![]() 的普通方程为
的普通方程为![]() ,以坐标原点为极点,
,以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(I)求直线![]() 的极坐标方程与曲线
的极坐标方程与曲线![]() 的参数方程;
的参数方程;
(II)设点D在曲线![]() 上,且曲线
上,且曲线![]() 在点D处的切线与直线
在点D处的切线与直线![]() 垂直,试确定点D的坐标.
垂直,试确定点D的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】计算题
(1)已知集合A={x|3<x<7},B={x|2<x<10},求A∪B,A∩B,RA
(2)计算下列各式 ① ![]()
②(2a ![]() b
b ![]() )(﹣6a
)(﹣6a ![]() b
b ![]() )÷(﹣3a
)÷(﹣3a ![]() b
b ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() .
.
(Ⅰ)求函数f(x)的定义域;
(Ⅱ)判定f(x)的奇偶性并证明;
(Ⅲ)用函数单调性定义证明:f(x)在(1,+∞)上是增函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数g(x)=3x , h(x)=9x .
(1)解方程:h(x)﹣8g(x)﹣h(1)=0;
(2)令p(x)= ![]() ,求值:p(
,求值:p( ![]() )+p(
)+p( ![]() )+…+p(
)+…+p( ![]() )+p(
)+p( ![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】原命题:“![]() ,
,![]() 为两个实数,若
为两个实数,若![]() ,则
,则![]() ,
,![]() 中至少有一个不小于1”,下列说法错误的是
中至少有一个不小于1”,下列说法错误的是
A.逆命题为:若![]() ,
,![]() 中至少有一个不小于1则
中至少有一个不小于1则![]() ,为假命题
,为假命题
B.否命题为:若![]() 则
则![]() ,
,![]() 都小于1 ,为假命题
都小于1 ,为假命题
C.逆否命题为:若![]() ,
,![]() 都小于1则
都小于1则![]() ,为真命题
,为真命题
D.“![]() ”是“
”是“![]() ,
,![]() 中至少有一个不小于1”的必要不充分条件
中至少有一个不小于1”的必要不充分条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】二手车经销商小王对其所经营的![]() 型号二手汽车的使用年数
型号二手汽车的使用年数![]() 与销售价格
与销售价格![]() (单位:万元/辆)进行整理,得到如下数据:
(单位:万元/辆)进行整理,得到如下数据:
使用年数 | 2 | 3 | 4 | 5 | 6 | 7 |
售价 | 20 | 12 | 8 | 6.4 | 4.4 | 3 |
| 3.00 | 2.48 | 2.08 | 1.86 | 1.48 | 1.10 |
下面是![]() 关于
关于![]() 的散点图:
的散点图:
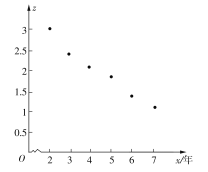
(I)由散点图看出,可以用线性回归模型拟合![]() 和
和![]() 的关系,请用相关系数加以说明;
的关系,请用相关系数加以说明;
(II)求![]() 关于
关于![]() 的回归方程,并预测某辆
的回归方程,并预测某辆![]() 型号二手汽车当使用年数为9年时,售价大约为多少?(
型号二手汽车当使用年数为9年时,售价大约为多少?(![]() 、
、![]() 的值精确到
的值精确到![]() )
)
(III)基于成本的考虑,该型号二手汽车的售价不得低于7118元,请根据(II)求出的回归方程预测在收购该型号二手汽车时,车辆的使用年数不得超过多少年?
参考公式: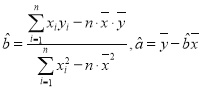 ,相关系数
,相关系数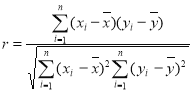 .
.
参考数据:![]() ,
,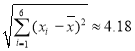 ,
,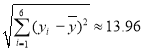 ,
,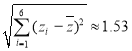 ,
,![]() ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com