
【题目】如图为一个摩天轮示意图。该摩天轮圆半径为4.8m,圆上最低点与地面距离为0.8m,60s转动一周.图中OA与地面垂直。以O为始边,逆时针转动0角到OB设B点与地面的距离为hm.

(1)求h与![]() 的函数解析式;
的函数解析式;
(2)设从OA开始转动,经过ts到达OB,求h与t的函数解析式.
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:高中数学 来源: 题型:
【题目】某县畜牧技术员张三和李四9年来一直对该县山羊养殖业的规模进行跟踪调查,张三提供了该县某山羊养殖场年养殖数量y(单位:万只)与相成年份x(序号)的数据表和散点图(如图所示),根据散点图,发现y与x有较强的线性相关关系,李四提供了该县山羊养殖场的个数z(单位:个)关于x的回归方程![]() .
.

(1)根据表中的数据和所给统计量,求y关于x的线性回归方程(参考统计量:![]() );
);
(2)试估计:①该县第一年养殖山羊多少万只?
②到第几年,该县山羊养殖的数量与第一年相比缩小了?
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知小李每次打靶命中靶心的概率都为40%,现采用随机模拟的方法估计小李三次打靶恰有两次命中靶心的概率.先由计算器产生0到9之间取整数值的随机数,指定0,1,2,3表示命中靶心,4,5,6,7,8,9表示未命中靶心,再以每三个随机数为一组,代表三次打靶的结果,经随机模拟产生了如下20组随机数:
321 421 191 925 271 932 800 478
589 663 531 297 396 021 546 388
230 113 507 965
据此估计,小李三次打靶恰有两次命中的概率为( )
A. 0.25 B. 0.30
C. 0.35 D. 0.40
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以5cm为单位长度作单位圆,分别作出![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 角的正弦线余弦线和正切线,量出它们的长度,写出这些角的正弦余弦和正切的近似值,再使用科学计算器求这些角的正弦余弦和正切,并进行比较.
角的正弦线余弦线和正切线,量出它们的长度,写出这些角的正弦余弦和正切的近似值,再使用科学计算器求这些角的正弦余弦和正切,并进行比较.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(题文)(题文)已知椭圆![]() 的离心率为
的离心率为![]() ,过右焦点
,过右焦点![]() 且斜率为1的直线交椭圆
且斜率为1的直线交椭圆![]() 于A,B两点, N为弦AB的中点,O为坐标原点.
于A,B两点, N为弦AB的中点,O为坐标原点.
(1)求直线ON的斜率![]() ;
;
(2)求证:对于椭圆![]() 上的任意一点M,都存在
上的任意一点M,都存在![]() ,使得
,使得![]() 成立.
成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
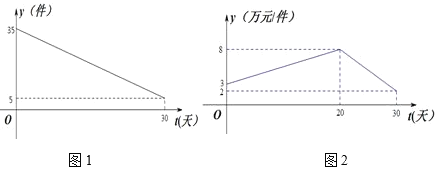
【题目】某商品近一个月内(30天)预计日销量![]() (件)与时间t(天)的关系如图1所示,单价
(件)与时间t(天)的关系如图1所示,单价![]() (万元/件)与时间t(天)的函数关系如图2所示,(t为整数)
(万元/件)与时间t(天)的函数关系如图2所示,(t为整数)
(1)试写出![]() 与
与![]() 的解析式;
的解析式;
(2)求此商品日销售额的最大值?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】容器中有![]()
![]() 种粒子,若相同种类的两颗粒子发生碰撞,则变成一颗
种粒子,若相同种类的两颗粒子发生碰撞,则变成一颗![]() 粒子;不同种类的两颗粒子发生碰撞,会变成另外一种粒子. 例如,一颗
粒子;不同种类的两颗粒子发生碰撞,会变成另外一种粒子. 例如,一颗![]() 粒子和一颗
粒子和一颗![]() 粒子发生碰撞则变成一颗
粒子发生碰撞则变成一颗![]() 粒子.现有
粒子.现有![]() 粒子
粒子![]() 颗,
颗,![]() 粒子
粒子![]() 颗,
颗,![]() 粒子
粒子![]() 颗,如果经过各种两两碰撞后,只剩
颗,如果经过各种两两碰撞后,只剩![]() 颗粒子. 给出下列结论:
颗粒子. 给出下列结论:
① 最后一颗粒子可能是![]() 粒子
粒子
② 最后一颗粒子一定是![]() 粒子
粒子
③ 最后一颗粒子一定不是![]() 粒子
粒子
④ 以上都不正确
其中正确结论的序号是________.(写出所有正确结论的序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com