
分析 (1)根据平面向量数量积的定义与夹角公式,即可求出$\overrightarrow{a}$、$\overrightarrow{b}$夹角的余弦值;
(2)【解法一】设$\overrightarrow{a}$、$\overrightarrow{b}$的夹角为θ,利用模长公式得出关于x的不等式(x2-1)+(2x-2)$\sqrt{2}$cosθ≥0,
讨论x=1、x>1和x<1时,求出cosθ的值,从而求出θ的值;
【解法二】设a与b的夹角为θ,由|$\overrightarrow{a}$+x$\overrightarrow{b}$|≥|$\overrightarrow{a}$+$\overrightarrow{b}$得出不等式x2+2$\sqrt{2}$xcosθ-2$\sqrt{2}$cosθ-1≥0对一切实数x恒成立,
利用判别式△≤0求出cosθ的值,从而得出θ的值.
解答 解:(1)因为|$\overrightarrow{a}$|=$\sqrt{2}$,|$\overrightarrow{b}$|=1,|$\overrightarrow{a}$-$\overrightarrow{b}$|=2,
所以|$\overrightarrow{a}$-$\overrightarrow{b}$|2=4,
即$\overrightarrow{a}$2-2$\overrightarrow{a}$•$\overrightarrow{b}$+$\overrightarrow{b}$2=4,
2-2$\overrightarrow{a}$•$\overrightarrow{b}$+1=4,
所以$\overrightarrow{a}$•$\overrightarrow{b}$=-$\frac{1}{2}$.
设$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为θ,
cosθ=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}|×|\overrightarrow{b}|}$=$\frac{-\frac{1}{2}}{\sqrt{2}×1}$=-$\frac{\sqrt{2}}{4}$ …(4分)
(2)【解法一】令$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为θ.
由|$\overrightarrow{a}$+x$\overrightarrow{b}$|≥|$\overrightarrow{a}$+$\overrightarrow{b}$|,得($\overrightarrow{a}$+x$\overrightarrow{b}$)2≥($\overrightarrow{a}$+$\overrightarrow{b}$)2,…(5分)
化为(x2-1)|$\overrightarrow{b}$|2+(2x-2)|$\overrightarrow{a}$|•|$\overrightarrow{b}$|cosθ≥0,
因为|$\overrightarrow{a}$|=$\sqrt{2}$,|$\overrightarrow{b}$|=1,
所以(x2-1)+(2x-2)$\sqrt{2}$cosθ≥0,…(6分)
当x=1时,式子显然成立; …(7分)
当x>1时,cosθ≥-$\frac{{x}^{2}-1}{(2x-2)\sqrt{2}}$=-$\frac{x+1}{2\sqrt{2}}$,
由于-$\frac{x+1}{2\sqrt{2}}$<-$\frac{\sqrt{2}}{2}$,故cosθ≥-$\frac{\sqrt{2}}{2}$;
当x<1时,cosθ≤-$\frac{{x}^{2}-1}{(2x-2)\sqrt{2}}$=-$\frac{x+1}{2\sqrt{2}}$,
由于-$\frac{x+1}{2\sqrt{2}}$>-$\frac{\sqrt{2}}{2}$,故cosθ≤-$\frac{\sqrt{2}}{2}$;
所以cosθ=-$\frac{\sqrt{2}}{2}$,解得θ=$\frac{3π}{4}$.…(12分)
【解法二】令$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为θ,由|$\overrightarrow{a}$+x$\overrightarrow{b}$|≥|$\overrightarrow{a}$+$\overrightarrow{b}$|,
得($\overrightarrow{a}$+x$\overrightarrow{b}$)2≥($\overrightarrow{a}$+$\overrightarrow{b}$)2,…(5分)
因为|$\overrightarrow{a}$|=$\sqrt{2}$,|$\overrightarrow{b}$|=1,
所以x2+2$\sqrt{2}$xcosθ-2$\sqrt{2}$cosθ-1≥0,
对一切实数x恒成立,…(7分)
所以△=8cos2θ+8$\sqrt{2}$cosθ+4≤0,…(9分)
即($\sqrt{2}$cosθ+1)2≤0,故cosθ=-$\frac{{\sqrt{2}}}{2}$,…(11分)
因为θ∈[0,π],所以θ=$\frac{3}{4}$π.…(12分)
点评 本题考查了平面向量的数量积与夹角公式的由于问题,也考查了不等式恒成立问题,是综合性题目.


 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:高中数学 来源: 题型:选择题
| A. | -x(1-x) | B. | x(1-x) | C. | -x(1+x) | D. | x(1+x) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
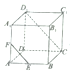 如图,在正方体中ABCD-A1B1C1D1,E、F分别为AB,AA1的中点.求证:
如图,在正方体中ABCD-A1B1C1D1,E、F分别为AB,AA1的中点.求证:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
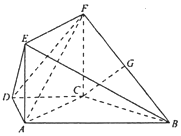 如图,在梯形ABCD中,AB∥CD,AB=4,AD=DC=CB=2,四边形ACFE是矩形,AE=1,平面ACFE⊥平面ABCD,点G是BF的中点.
如图,在梯形ABCD中,AB∥CD,AB=4,AD=DC=CB=2,四边形ACFE是矩形,AE=1,平面ACFE⊥平面ABCD,点G是BF的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com