
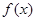 在定义域内存在区间
在定义域内存在区间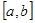 ,满足
,满足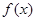 在
在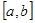 上的值域为
上的值域为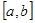 ,则称这样的函数
,则称这样的函数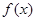 为“优美函数”.
为“优美函数”.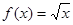 是否为“优美函数”?若是,求出
是否为“优美函数”?若是,求出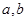 ;若不是,说明理由;
;若不是,说明理由;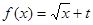 为“优美函数”,求实数
为“优美函数”,求实数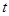 的取值范围.
的取值范围.科目:高中数学 来源:不详 题型:解答题
 ,若
,若 在点
在点 处的切线斜率为
处的切线斜率为 .
. 表示
表示 ;
; ,若
,若 对定义域内的
对定义域内的 恒成立,
恒成立, 的取值范围;
的取值范围;  ,证明:
,证明: .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 ,若存在区间
,若存在区间 ,使得
,使得 ,则称区间
,则称区间 为函数
为函数 的一个“稳定区间”.给出下列3个函数:
的一个“稳定区间”.给出下列3个函数: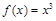 ; ②
; ②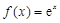 ; ③
; ③ .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 米,宽
米,宽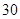 米的长方形体育馆.按照建筑要求,每隔
米的长方形体育馆.按照建筑要求,每隔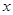 米(
米( ,
,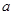 为正常数)需打建一个桩位,每个桩位需花费
为正常数)需打建一个桩位,每个桩位需花费 万元(桩位视为一点且打在长方形的边上),桩位之间的
万元(桩位视为一点且打在长方形的边上),桩位之间的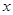 米墙面需花
米墙面需花 万元,在不计地板和天花板的情况下,当
万元,在不计地板和天花板的情况下,当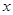 为何值时,所需总费用最少?
为何值时,所需总费用最少?查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 是定义在正整数集上的函数,且
是定义在正整数集上的函数,且 满足:“当
满足:“当 成立时,总可推出
成立时,总可推出 成立”,那么,下列命题总成立的是( )
成立”,那么,下列命题总成立的是( )A.若 成立,则 成立,则 成立 成立 |
B.若 成立,则当 成立,则当 时,均有 时,均有 成立 成立 |
C.若 成立,则 成立,则 成立 成立 |
D.若 成立,则当 成立,则当 时,均有 时,均有 成立 成立 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com